logo

chenjie04's blog

扩散模型（Diffusion Model）学习笔记

2022-12-28 Views8796字50 min read繁

一、先验知识

1、条件概率的一般形式

P(A,B,C)=P(C∣B,A)P(B,A)=P(C∣B,A)P(B∣A)P(A)P(A,B,C) = P(C|B,A)P(B,A) = P(C|B,A)P(B|A)P(A)

P(B,C∣A)=P(B∣A)P(C∣A,B)P(B,C|A) = P(B|A)P(C|A,B)

证明：
左边：P(B,C∣A)=P(A,B,C)/P(A)P(B,C|A) = P(A,B,C) / P(A)
右边：P(B∣A)=P(A,B)/P(A)P(B|A) = P(A,B) / P(A); 而 P(C∣A,B)=P(A,B,C)/P(A,B)P(C|A,B) = P(A,B,C) / P(A,B); 两项相乘得：P(A,B,C)/P(A)P(A,B,C) / P(A)

2、基于马尔可夫假设的条件概率

如果满足马尔可夫链关系A->B->C， 那么有

P(A,B,C)=P(C∣B,A)P(B,A)=P(C∣B)P(B∣A)P(A)P(B,C∣A)=P(B∣A)P(C∣B)P(A,B,C) = P(C|B,A)P(B,A) = P(C|B)P(B|A)P(A)\\ P(B,C|A) = P(B|A)P(C|B)

因为马尔可夫的性质就是当前时刻的状态只与前一时刻有关，即C只与B相关，B只与A相关

3、高斯分布的KL散度公式

对于两个单一变量的高斯分布p和q而言，它们的KL散度为

KL(p,q)=logσ2σ1+σ12+(μ1−μ2)22σ22−12KL(p,q) = log \frac{\sigma _{2}}{\sigma _{1}} + \frac{\sigma ^{2}_{1} + (\mu _{1} - \mu _{2})^{2}}{2 \sigma ^{2}_{2}} - \frac{1}{2}

4、重参数技巧 (很重要)

若希望从高斯分布 N(μ,σ2)N(\mu , \sigma ^{2})中采样， 可以先从标准正态分布 N(0,1)N(0 , 1 )采样出 ϵ\epsilon，再通过σ∗ϵ+μ\sigma \ast \epsilon + \mu得到采样结果。这样做的好处的将随机性转移到了 ϵ\epsilon这个常量上，而σ\sigma和μ\mu则当作仿射变换网络的一部分。

二、Diffusion Model

如下图所示，扩散模型定义了一个马尔可夫链：

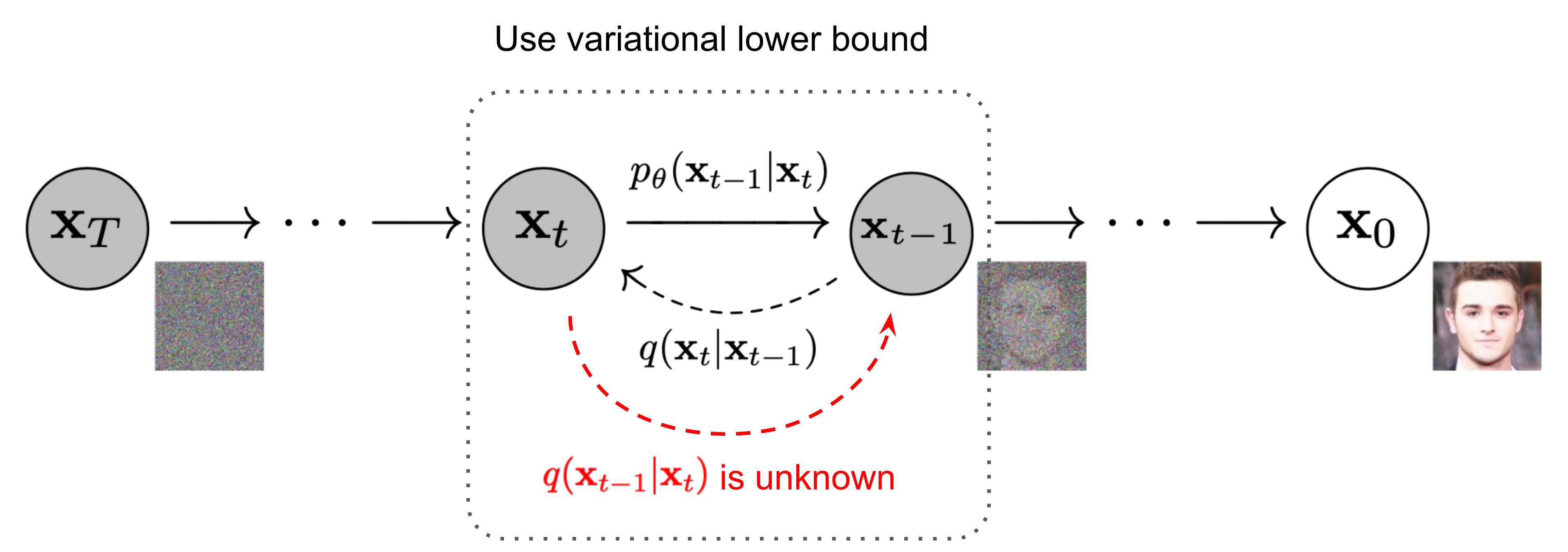
在扩散过程 (x0→xT)(\mathbf{x}_0 \rightarrow \mathbf{x}_T) 中，慢慢地给原始图片（或者叫原始数据分布）添加高斯噪声，x0\mathbf{x}_0 表示从真实数据集中采样得到的一张图片，对x0\mathbf{x}_0 添加TT次噪声，随着噪声的不断添加，图片逐渐变得模糊，当TT足够大时，最终数据分布就变成了一个各项独立的高斯分布，即xT\mathbf{x}_T为标准正态分布。在训练过程中，每次添加的噪声是已知的，即q(xt∣xt−1)q(\mathbf{x}_t | \mathbf{x}_{t-1})是已知的，根据马尔科夫链的性质，可以递归得到q(xt∣x0)q(\mathbf{x}_t | \mathbf{x}_{0})，即扩散过程是已知的。

我们需要学习的是逆扩散过程(xT→x0)(\mathbf{x}_T \rightarrow \mathbf{x}_0)，从噪声中构建出原来的图片。假如我们能够在给定xt\mathbf{x}_t的条件下计算出xt−1\mathbf{x}_{t-1}，即知道q(xt−1∣xt)q(\mathbf{x}_{t-1} | \mathbf{x}_t)，那我们就能够从任意一张噪声图片中经过一次次的采样得到一张图片而达成图片生成的目的。不幸的是我们很难估计q(xt−1∣xt)q(\mathbf{x}_{t-1} | \mathbf{x}_t)，因为它需要用整个数据集来估计，所以我们希望能够用一个神经网络pθ(xt−1∣xt)p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_t)来近似这个逆扩散过程q(xt−1∣xt)q(\mathbf{x}_{t-1} | \mathbf{x}_t)。

下面进行扩散过程与逆扩散过程的推导。

1、扩散过程

给定初始数据分布x0∼q(x)\mathbf{x}_{0} \sim q(\mathbf{x})， 我们定义一个马尔科夫链的前向扩散过程，该过程中的每个时间步tt我们慢慢地向分布中添加高斯噪声，该噪声的标准差是由固定值βt\beta_{t}确定，均值由βt\beta_{t}和当前时刻的数据xt\mathbf{x}_{t}决定。βt\beta_{t}定义为(0,1)(0,1)的小数，即{βt∈(0,1)}t=1t\{ \beta_{t} \in (0,1)\}_{t=1}^{t}，那么这个扩散过程可以记为

q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)q(\mathbf{x}_{t}|\mathbf{x}_{t-1})= \mathcal{N}(\mathbf{x}_{t};\sqrt{1-\beta_{t}}\mathbf{x}_{t-1},\beta_{t}\textbf{I})

根据基于马尔可夫假设的条件概率公式，有

q(x1:T∣x0)=∏t=1Tq(xt∣xt−1)q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) = \prod_{t=1}^{T} q(\mathbf{x}_{t}|\mathbf{x}_{t-1})

随着时间tt逐渐增大，初始数据分布逐渐失去其具有判别性的特征；当T→∞T \to \infty，最终数据分布xT\mathbf{x}_{T}就等价于一个各向独立的高斯分布。

在扩散过程中，一般而言是一步一步迭代来算出每一步的噪声样本，即根据x0\mathbf{x}_{0}计算x1\mathbf{x}_{1}，根据x1\mathbf{x}_{1}计算x2\mathbf{x}_{2}，……，一直迭代直到xT\mathbf{x}_{T}。但是，实际上利用重参数技巧，我们完全可以基于x0\mathbf{x}_{0}和βt\beta_{t}计算出任意时刻的xt\mathbf{x}_{t}，而不需要做迭代。

要求噪声样本xt\mathbf{x}_{t}，就得从分布N(1−βtxt−1,βtI)\mathcal{N}(\sqrt{1-\beta_{t}} \mathbf{x}_{t-1},\beta_{t}\textbf{I})中抽样，根据重参数技巧，我们可以先从标准正态分布N(0,I)\mathcal{N}(\textbf{0},\textbf{I})中采样出ϵt−1\epsilon_{t-1}，然后根据重参数技巧得xt=1−βtxt−1+βtϵt−1\mathbf{x}_{t}=\sqrt{1-\beta_{t}}\mathbf{x}_{t-1}+\beta_{t} \epsilon_{t-1}，为简化公式，记αt=1−βt\alpha_{t} = 1 - \beta_{t}，则有

xt=αtxt−1+1−αtϵt−1;      where ϵt−1∼N(0,I)\mathbf{x}_{t}=\sqrt{\alpha_{t}} \mathbf{x}_{t-1}+\sqrt{1-\alpha_{t}}\epsilon_{t-1}; \ \ \ \ \ \ where \ \epsilon_{t-1} \sim \mathcal{N}(\textbf{0},\textbf{I})

同理，

xt−1=αt−1xt−2+1−αt−1ϵt−2;      where ϵt−2∼N(0,I)\mathbf{x}_{t-1}=\sqrt{\alpha_{t-1}} \mathbf{x}_{t-2}+\sqrt{1-\alpha_{t-1}}\epsilon_{t-2}; \ \ \ \ \ \ where \ \epsilon_{t-2} \sim \mathcal{N}(\textbf{0},\textbf{I})

把xt−1\mathbf{x}_{t-1}代入上式，则有

xt=αtαt−1xt−2+αt(1−αt−1)ϵt−2+1−αtϵt−1;\mathbf{x}_{t} =\sqrt{\alpha_{t}\alpha_{t-1}}\mathbf{x}_{t-2}+\sqrt{\alpha_{t}(1-\alpha_{t-1})}\epsilon_{t-2}+\sqrt{1-\alpha_{t}}\epsilon_{t-1};

注意，两个正态分布x∼N(μ1,σ12)\mathbf{x} \sim \mathcal{N}(\mu_{1},\sigma_{1}^{2})和Y∼N(μ2,σ22)Y \sim \mathcal{N}(\mu_{2},\sigma_{2}^{2})叠加后的分布ax+bYa\mathbf{x} + bY的均值为μ=aμ1+bμ2\mu = a\mu_{1} + b\mu_{2}，方差为σ2=a2σ12+b2σ22\sigma^{2} = a^{2}\sigma_{1}^{2} + b^{2}\sigma_{2}^{2}。由于ϵt−1\epsilon_{t-1}和ϵt−2\epsilon_{t-2}是标准正态分布，即N(0,I)\mathcal{N}(\textbf{0},\textbf{I})， 因此αt(1−αt−1)ϵt−2+1−αtϵt−1∼N(0,(1−αtαt−1)I)\sqrt{\alpha_{t}(1-\alpha_{t-1})}\epsilon_{t-2}+\sqrt{1-\alpha_{t}}\epsilon_{t-1} \sim \mathcal{N}(\textbf{0},(1-\alpha_{t}\alpha_{t-1})\textbf{I})，根据重参数技巧，我们重新在标准正态分布中采样一个新的噪声ϵˉt−2\bar{\epsilon}_{t-2}，则有αt(1−αt−1)ϵt−2+1−αtϵt−1=(1−αtαt−1)ϵˉt−2\sqrt{\alpha_{t}(1-\alpha_{t-1})}\epsilon_{t-2}+\sqrt{1-\alpha_{t}}\epsilon_{t-1} = \sqrt{(1-\alpha_{t}\alpha_{t-1})}\bar{\epsilon}_{t-2}

也即是

xt=αtαt−1xt−2+(1−αtαt−1)ϵˉt−2;\mathbf{x}_{t} =\sqrt{\alpha_{t}\alpha_{t-1}}\mathbf{x}_{t-2} + \sqrt{(1-\alpha_{t}\alpha_{t-1})}\bar{\epsilon}_{t-2};

继续迭代下去，不难看出

xt=αtαt−1αt−2xt−3+(1−αtαt−1αt−2)ϵˉt−3;…\mathbf{x}_{t} =\sqrt{\alpha_{t}\alpha_{t-1}\alpha_{t-2}}\mathbf{x}_{t-3} + \sqrt{(1-\alpha_{t}\alpha_{t-1}\alpha_{t-2})}\bar{\epsilon}_{t-3};\\ \dots

我们记αˉt=∏i=1Tαi\bar{\alpha}_{t}=\prod_{i=1}^{T} \alpha_{i}，另外，由于ϵˉt−2,ϵˉt−3,…\bar{\epsilon}_{t-2}, \bar{\epsilon}_{t-3}, \dots均为服从标准正态分布的噪声可简单记为ϵ\epsilon，最终可得出

xt=αˉtx0+(1−αˉtϵ;\mathbf{x}_{t} =\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0} + \sqrt{(1-\bar{\alpha}_{t}}\epsilon;\\

即可以基于x0\mathbf{x}_{0}和βt\beta_{t}计算出任意时刻的xt\mathbf{x}_{t}，

q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)q(\mathbf{x}_{t}|\mathbf{x}_{0}) = \mathcal{N}(\mathbf{x}_{t};\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0},(1-\bar{\alpha}_{t})\textbf{I})

至此，Diffusion model的扩散过程结束，另外，一般来说对于超参数βt\beta_{t}的设置一开始时设置得比较小，不要一下子就完全打乱原始数据的分布，当数据分布越来越接近高斯噪声时，我们就可以把βt\beta_{t}设置得大一些，即β1<β2<⋯<βT\beta_{1} < \beta_{2} < \dots < \beta_{T}。

2、逆扩散过程（Reverse Process）

正如前面提到逆扩散过程正是要求q(xt−1∣xt)q(\mathbf{x}_{t-1} | \mathbf{x}_t)，但是很难，因此采用神经网络pθ(xt−1∣xt)p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_t)来近似。实际上，pθ(xt−1∣xt)p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_t) 也是一个从高斯分布中采样的过程，该高斯分布的均值与噪声样本xt\mathbf{x}_t以及实践tt相关，记为μθ(xt,t)\mu _{\theta}(\mathbf{x}_t,t)，方差同理，记为Σθ(xt,t)\Sigma _{\theta}(\mathbf{x}_t,t)，则

pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu _{\theta}(\mathbf{x}_t,t), \Sigma _{\theta}(\mathbf{x}_t,t))

但是，我们还是不知道该怎么求。巧妙的是，虽然我们不知道q(xt−1∣xt)q(\mathbf{x}_{t-1} | \mathbf{x}_t)，但是q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)是可知的，可以用q(xt∣x0)q(\mathbf{x}_t | \mathbf{x}_0)，q(xt−1∣x0)q(\mathbf{x}_{t-1} | \mathbf{x}_0)和q(xt∣xt−1)q(\mathbf{x}_{t}|\mathbf{x}_{t-1})表示，也就是说引入x0\mathbf{x}_0这个问题就可解了，因此考虑用q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)监督pθ(xt−1∣xt)p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_t)的学习。

首先来看q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)的推导，根据条件概率公式有

q(xt−1∣xt,x0)=q(x0xt−1xt)q(x0xt)q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) = \frac{q(\mathbf{x}_0\mathbf{x}_{t-1}\mathbf{x}_t)}{q(\mathbf{x}_0\mathbf{x}_t)}

上下同乘q(x0xt−1)q(\mathbf{x}_0\mathbf{x}_{t-1})得

=q(x0xt−1xt)q(x0xt−1)⋅q(x0xt−1)q(x0xt)= \frac{q(\mathbf{x}_0 \mathbf{x}_{t-1} \mathbf{x}_t)}{q(\mathbf{x}_0 \mathbf{x}_{t-1})} \cdot \frac{q(\mathbf{x}_0\mathbf{x}_{t-1})}{q(\mathbf{x}_0\mathbf{x}_{t})}

第一项等于q(xt∣xt−1x0)q(\mathbf{x}_t | \mathbf{x}_{t-1}\mathbf{x}_0)，又因为扩散过程是马尔可夫过程，所以q(xt∣xt−1x0)=q(xt∣xt−1)q(\mathbf{x}_t | \mathbf{x}_{t-1}\mathbf{x}_0)=q(\mathbf{x}_t | \mathbf{x}_{t-1})；第二项上下同除q(x0)q(\mathbf{x}_0)，同样根据条件概率公式有，q(x0xt−1)q(x0xt)=q(x0xt−1)/q(x0)q(x0xt)/q(x0)=q(xt−1∣x0)q(xt∣x0)\frac{q(\mathbf{x}_0\mathbf{x}_{t-1})}{q(\mathbf{x}_0\mathbf{x}_{t})} = \frac{q(\mathbf{x}_0\mathbf{x}_{t-1}) / q(\mathbf{x}_0)}{q(\mathbf{x}_0\mathbf{x}_{t}) / q(\mathbf{x}_0)} = \frac{q(\mathbf{x}_{t-1} | \mathbf{x}_0)}{q(\mathbf{x}_t | \mathbf{x}_0)}，因此，

q(xt−1∣xt,x0)=q(xt∣xt−1)⋅q(xt−1∣x0)q(xt∣x0)q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) = q(\mathbf{x}_t | \mathbf{x}_{t-1}) \cdot \frac{q(\mathbf{x}_{t-1} | \mathbf{x}_0)}{q(\mathbf{x}_t | \mathbf{x}_0)}

可以看到这三项都是扩散过程，根据前面扩散过程的推导以及高斯分布的概率密度函数有，

q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)=1σ2π(1−αt)e−12(xt−αtxt−1)21−αt;  where αt=1−βtq(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_{t};\sqrt{1-\beta _{t}}\mathbf{x}_{t-1},\beta_{t}\textbf{I}) = \frac{1}{\sigma \sqrt{2 \pi (1-\alpha _t)}} e ^{- \frac{1}{2} \frac{(\mathbf{x}_t - \sqrt{\alpha _t} \mathbf{x}_{t-1})^2}{ 1-\alpha _t}}; \ \ where \ \alpha _t = 1-\beta _{t}

q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)=1σ2π(1−αˉt)e−12(xt−αˉtx0)21−αˉt;  where αˉt=∏i=1Tαiq(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t};\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0},(1-\bar{\alpha}_{t})\textbf{I}) = \frac{1}{\sigma \sqrt{2 \pi (1-\bar{\alpha}_{t})}} e ^{- \frac{1}{2} \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0})^2}{ 1-\bar{\alpha}_{t}}}; \ \ where \ \bar{\alpha}_{t}=\prod_{i=1}^{T} \alpha_{i}

q(xt−1∣x0)=N(xt−1;αˉt−1x0,(1−αˉt−1)I)=1σ2π(1−αˉt−1)e−12(xt−1−αˉt−1x0)21−αˉt−1;q(\mathbf{x}_{t-1} | \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1};\sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_{0},(1-\bar{\alpha}_{t-1})\textbf{I}) = \frac{1}{\sigma \sqrt{2 \pi (1-\bar{\alpha}_{t-1})}} e ^{- \frac{1}{2} \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_{0})^2}{ 1-\bar{\alpha}_{t-1}}};

注：若随机变数x\mathbf{x}服从一个均值为μ\mu 、标准差为σ\sigma的正态分布，记为：

x∼N(μ,σ2),f(x)=1σ2πe−(x−μ)22σ2\mathbf{x} \sim \mathcal{N}(\mu, \sigma ^{2}), f(x) = \frac{1}{\sigma \sqrt{2 \pi}} e ^{- \frac{(x-\mu)^2}{2 \sigma ^2}}

因此，

q(xt−1∣xt,x0)=q(xt∣xt−1)⋅q(xt−1∣x0)q(xt∣x0)∝exp(−12((xt−αtxt−1)2βt+(xt−1−αˉt−1x0)21−αˉt−1+(xt−αˉtx0)21−αˉt))=exp(−12(xt2−2αtxtxt−1+αtxt−12βt+xt−12−2αˉt−1x0xt−1+αˉt−1x021−αˉt−1−(xt−αˉtx0)21−αˉt))=exp(−12((αtβt+11−αˉt−1)xt−12−2(αtβtxt+αˉt−11−αˉt−1x0)xt−1+C(xt,x0)))\begin{aligned} q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) &= q(\mathbf{x}_t | \mathbf{x}_{t-1}) \cdot \frac{q(\mathbf{x}_{t-1} | \mathbf{x}_0)}{q(\mathbf{x}_t | \mathbf{x}_0)} \\ &\propto exp (- \frac{1}{2} (\frac{(\mathbf{x}_t - \sqrt{\alpha _t} \mathbf{x}_{t-1}) ^2}{\beta _t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0)^2}{1- \bar{\alpha} _{t-1}} + \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t}\mathbf{x}_0)^2}{1-\bar{\alpha}_t})) \\ &= exp(- \frac{1}{2} (\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha _t}\mathbf{x}_t {\color{red}{\mathbf{x}_{t-1}}} + \alpha _t {\color{green}{\mathbf{x}_{t-1}^2}}}{\beta _t} + \frac{{\color{green}{\mathbf{x}_{t-1}^2}} - 2\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0 {\color{red}{\mathbf{x}_{t-1}}} + \bar{\alpha}_{t-1}\mathbf{x}_0^2}{1-\bar{\alpha}_{t-1}}- \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t}\mathbf{x}_0)^2}{1-\bar{\alpha}_t})) \\ &=exp(-\frac{1}{2}({\color{green}{(\frac{\alpha _t}{\beta _t}+\frac{1}{1-\bar{\alpha}_{t-1}})\mathbf{x}_{t-1}^{2}}}-{\color{red}{2(\frac{\sqrt{\alpha_t}}{\beta_t}\mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}\mathbf{x}_0)\mathbf{x}_{t-1}}}+C(\mathbf{x}_t,\mathbf{x}_0))) \end{aligned}

其中，C(xt,x0)C(\mathbf{x}_t,\mathbf{x}_0)是不包含xt−1\mathbf{x}_{t-1}的函数，因此细节可以忽略。然后将式子中的每一项除以(αtβt+11−αˉt−1)(\frac{\alpha _t}{\beta _t}+\frac{1}{1-\bar{\alpha}_{t-1}})构造成正态分布密度函数形式，可得

=exp(−12(xt−1−(αtβtxt+αˉt−11−αˉt−1x0)/(αtβt+11−αˉt−1))21/(αtβt+11−αˉt−1))=exp(-\frac{1}{2} \frac{(\mathbf{x}_{t-1}-(\frac{\sqrt{\alpha_t}}{\beta_t}\mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}\mathbf{x}_0)/(\frac{\alpha _t}{\beta _t}+\frac{1}{1-\bar{\alpha}_{t-1}}))^2}{1 / (\frac{\alpha _t}{\beta _t}+\frac{1}{1-\bar{\alpha}_{t-1}})})

所以，q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)服从正态分布，方差与均值如下所示 ( 注意： αt=1−βt,αˉt=∏i=1Tαi\alpha _t = 1- \beta _t, \bar{\alpha} _t = \prod_{i=1}^{T} \alpha_{i} )，

q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t\textbf{I})

β~t=1/(αtβt+11−αˉt−1)=1/(αt−αˉt+βtβt(1−αˉt−1))=1−αˉt−11−αˉt⋅βt\tilde{\beta}_t = 1 / (\frac{\alpha _t}{\beta _t}+\frac{1}{1-\bar{\alpha}_{t-1}}) = 1/ (\frac{\alpha_t - \bar{\alpha}_t + \beta _t}{\beta _t (1- \bar{\alpha}_{t-1})}) = {\color{magenta}{\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t}}

μ~(xt,x0)=(αtβtxt+αˉt−11−αˉt−1x0)/(αtβt+11−αˉt−1)=(αtβtxt+αˉt−11−αˉt−1x0)⋅1−αˉt−11−αˉt⋅βt=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉtx0\begin{aligned} \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0) &= (\frac{\sqrt{\alpha_t}}{\beta_t}\mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}\mathbf{x}_0)/(\frac{\alpha _t}{\beta _t}+\frac{1}{1-\bar{\alpha}_{t-1}}) \\ &= (\frac{\sqrt{\alpha_t}}{\beta_t}\mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}\mathbf{x}_0) \cdot {\color{magenta}{\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t}} \\ &= \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0 \end{aligned}

由扩散过程可知 xt=αˉtx0+(1−αˉtϵt\mathbf{x}_{t} =\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0} + \sqrt{(1-\bar{\alpha}_{t}}\epsilon_t，即x0=1αˉt(xt−(1−αˉtϵt)\mathbf{x}_{0} =\frac{1}{\sqrt{\bar{\alpha}_{t}} }(\mathbf{x}_{t} - \sqrt{(1-\bar{\alpha}_{t}}\epsilon_t)，代入上式可得（注意：αˉt=αˉt−1⋅αt\bar{\alpha}_t = \bar{\alpha}_{t-1} \cdot \alpha_t）

μ~(xt,x0)=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉt1αˉt(xt−(1−αˉtϵt)=1αt(xt−1−αt1−αˉtϵt)\begin{aligned} \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0) &= \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_{t}} }(\mathbf{x}_{t} - \sqrt{(1-\bar{\alpha}_{t}}\epsilon_t) \\ &= \frac{1}{\sqrt{\alpha _t}}(\mathbf{x}_t - \frac{1-\alpha _t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_t) \end{aligned}

因此，

q(xt−1∣xt,x0)=N(xt−1;1αt(xt−1−αt1−αˉtϵt),1−αˉt−11−αˉt⋅βtI)q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha _t}}(\mathbf{x}_t - \frac{1-\alpha _t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_t), \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t\textbf{I})

接下来，我们就可以利用q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)来监督pθ(xt−1∣xt)p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)的训练了！

3、损失函数

要优化模型pθ(xt−1∣xt)p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)可以考虑最大化对数似然概率，即最小化负的对数似然概率−logpθ(x0)-logp\theta(\mathbf{x}_0)（为什么是x0\mathbf{x}_0？因为扩散过程的马尔科夫链），但是由于很难对噪声空间进行积分，因此直接优化−logpθ(x0)-logp\theta(\mathbf{x}_0)是困难的，因此，向VAE一样，转而去优化它的变分下界LVLBL_{VLB}，

我们知道KL散度是两个概率分布差别的非对称性度量，即KL散度大于等于零，因此有

−logpθ(x0)≤−logpθ(x0)+DKL(q(x1:T∣x0)∣∣pθ(x1:T∣x0))=−logpθ(x0)+Ex1:T∼q(x1:T∣x0)[logq(x1:T∣x0)pθ(x0:T)/pθ(x0)]=−logpθ(x0)+Eq[logq(x1:T∣x0)pθ(x0:T)+logpθ(x0)]=Eq[logq(x1:T∣x0)pθ(x0:T)]\begin{aligned} -logp\theta(\mathbf{x}_0) &\le -logp\theta(\mathbf{x}_0) + D_{KL}(q(\mathbf{x}_{1:T}|\mathbf{x}_0)||p\theta(\mathbf{x}_{1:T}|\mathbf{x}_0)) \\ &= -logp\theta(\mathbf{x}_0) + \mathbb{E}_{\mathbf{x}_{1:T} \sim q(\mathbf{x}_{1:T}|\mathbf{x}_0) }[log \frac{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}{p _{\theta} (\mathbf{x}_{0:T}) / p _{\theta} (\mathbf{x}_0)}] \\ &= -logp\theta(\mathbf{x}_0) + \mathbb{E}_q [log \frac{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}{p _{\theta} (\mathbf{x}_{0:T})} + log p _{\theta} (\mathbf{x}_0)] \\ &= \mathbb{E}_q [log \frac{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}{p _{\theta} (\mathbf{x}_{0:T})} ] \end{aligned}

其中，Eq[logq(x1:T∣x0)pθ(x0:T)]\mathbb{E}_q [log \frac{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}{p _{\theta} (\mathbf{x}_{0:T})} ]就是负对数似然的变分下界。或者从另外一个角度，我们可以优化真实分布与预测分布的交叉熵（cross entropy），但是由于同样的原因，优化很困难，因此求变分下界，

LCE=−Eq(x0)logpθ(x0)=−Eq(x0)log(∫pθ(x0:T)dx1:T)=−Eq(x0)log(∫q(x1:T∣x0)pθ(x0:T)q(x1:T∣x0)dx1:T)=−Eq(x0)log(Eq(x1:T∣x0)pθ(x0:T)q(x1:T∣x0))≤−Eq(x0:T)logpθ(x0:T)q(x1:T∣x0)=Eq(x0:T)logq(x1:T∣x0)pθ(x0:T)\begin{aligned} L_{CE} &= - \mathbb{E} _{q(\mathbf{x}_0)} log p _{\theta} (\mathbf{x}_0) \\ &= - \mathbb{E} _{q(\mathbf{x}_0)} log (\int p _{\theta} (\mathbf{x}_{0:T})d_{\mathbf{x}_{1:T}}) \\ &= - \mathbb{E} _{q(\mathbf{x}_0)} log (\int q(\mathbf{x}_{1:T}|\mathbf{x}_0) \frac{p _{\theta} (\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0) }d_{\mathbf{x}_{1:T}}) \\ &= - \mathbb{E} _{q(\mathbf{x}_0)} log (\mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_0)} \frac{p _{\theta} (\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0) }) \\ &\le - \mathbb{E}_{q(\mathbf{x}_{0:T})} log \frac{p _{\theta} (\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0) }\\ &= \mathbb{E}_{q(\mathbf{x}_{0:T})} log \frac{q(\mathbf{x}_{1:T}|\mathbf{x}_0) }{p _{\theta} (\mathbf{x}_{0:T})} \end{aligned}

为了方程中的每个项可解析计算，可以进一步将目标重写为几个KL散度和熵项的组合，

LVLB=Eq(x0T)[log⁡q(x1:T∣x0)pθ(x0:T)]=Eq[log⁡∏t=1Tq(xt∣xt−1)pθ(xT)∏t=1Tpθ(xt−1∣xt)]=Eq[−log⁡pθ(xT)+∑t=1Tlog⁡q(xt∣xt−1)pθ(xt−1∣xt)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt∣xt−1)pθ(xt−1∣xt)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡(q(xt−1∣xt,x0)pθ(xt−1∣xt)⋅q(xt∣x0)q(xt−1∣x0))+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)+∑t=2Tlog⁡q(xt∣x0)q(xt−1∣x0)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)+log⁡q(xT∣x0)q(x1∣x0)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[log⁡q(xT∣x0)pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)−log⁡pθ(x0∣x1)]=Eq[DKL(q(xT∣x0)∥pθ(xT))⎵LT+∑t=2TDKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))⎵Lt−1−log⁡pθ(x0∣x1)⎵L0]\begin{aligned} & L_{\mathrm{VLB}}=\mathbb{E}_{q(\mathbf{x} 0 T)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \\ & =\mathbb{E}_q\left[\log \frac{\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_T\right) \prod_{t=1}^T p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=1}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \left(\frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)} \cdot \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}\right)+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_T\right)}+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)\right] \\ & =\mathbb{E}_q[\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_T\right)\right)}_{L_T}+\sum_{t=2}^T \underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\right)}_{L_{t-1}}-\underbrace{\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}_{L_0}] \\ & \end{aligned}

变分下界可以简单表示如下：

LVLB=LT+LT−1+⋯+L0 where LT=DKL(q(xT∣x0)∥pθ(xT))Lt=DKL(q(xt∣xt+1,x0)∥pθ(xt∣xt+1)) for 1≤t≤T−1L0=−log⁡pθ(x0∣x1)\begin{aligned} L_{\mathrm{VLB}} & =L_T+L_{T-1}+\cdots+L_0 \\ \text { where } L_T & =D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_T\right)\right) \\ L_t & =D_{\mathrm{KL}}\left(q\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}\right)\right) \text { for } 1 \leq t \leq T-1 \\ L_0 & =-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right) \end{aligned}

其中，因为qq没有参数且xT\mathbf{x}_T是高斯噪声，所以LTL_T是常数，再训练的时候可以省略；另外，Denoising Diffusion Probabilistic Models（DDPM）使用一个单独的解码器N(x0;μθ(x1,1),Σθ(x1,1))\mathcal{N}(\mathbf{x}_0; \mu _\theta (\mathbf{x}_1,1), \Sigma _\theta (\mathbf{x}_1,1))来建模L0L_0，而不是计算KL散度。

4、损失函数的重参数化

总的来说，我们希望可以学习一个神经网络可以近似逆扩散过程的条件概率分布，该神经网络表示为 pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))p _\theta (\mathbf{x}_{t-1} | \mathbf{x}_t) = \mathcal{N} (\mathbf{x}_{t-1}; \mu _\theta (\mathbf{x}_t, t), \Sigma _\theta (\mathbf{x}_t, t))。我们希望训练μθ\mu _\theta来预测μ~t=1αt(xt−1−αt1−αˉtϵt)\tilde{\mu}_t = \frac{1}{\sqrt{\alpha _t}}(\mathbf{x}_t - \frac{1-\alpha _t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_t)。因为，xt\mathbf{x}_t在训练的过程中是已知的，所以我们的神经网络可以直接基于xt\mathbf{x}_t在时间步tt预测高斯噪声ϵt\epsilon _t，

μθ(xt,t)=1αt(xt−1−αt1−αˉtϵθ(xt,t)) Thus xt−1=N(xt−1;1αt(xt−1−αt1−αˉtϵθ(xt,t)),Σθ(xt,t))\begin{aligned} \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right) & =\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_\theta\left(\mathbf{x}_t, t\right)\right) \\ \text { Thus } \mathbf{x}_{t-1} & =\mathcal{N}\left(\mathbf{x}_{t-1} ; \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right), \mathbf{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right) \end{aligned}

损失函数LtL_t最终可以重参数化来最小化均值μ~\tilde{\mu}的差异,

Lt=Ex0,ϵ[12∥Σθ(xt,t)∥22∥μ~t(xt,x0)−μθ(xt,t)∥2]=Ex0,ϵ[12∥Σθ∥22∥1αt(xt−1−αt1−αˉtϵt)−1αt(xt−1−αt1−αˉtϵθ(xt,t))∥2]=Ex0,ϵ[(1−αt)22αt(1−αˉt)∥Σθ∥22∥ϵt−ϵθ(xt,t)∥2]=Ex0,ϵ[(1−αt)22αt(1−αˉt)∥Σθ∥22∥ϵt−ϵθ(αˉtx0+1−αˉtϵt,t)∥2]\begin{aligned} L_t & =\mathbb{E}_{\mathbf{x}_{0,} \epsilon}\left[\frac{1}{2\left\|\mathbf{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right\|_2^2}\left\|\tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right)-\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_{0,} \epsilon}\left[\frac{1}{2\left\|\mathbf{\Sigma}_\theta\right\|_2^2}\left\|\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_t\right)-\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x} 0, \epsilon}\left[\frac{\left(1-\alpha_t\right)^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\left\|\mathbf{\Sigma}_\theta\right\|_2^2}\left\|\epsilon_t-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_{0,} \epsilon}\left[\frac{\left(1-\alpha_t\right)^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\left\|\mathbf{\Sigma}_\theta\right\|_2^2}\left\|\epsilon_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \epsilon_t, t\right)\right\|^2\right] \end{aligned}

另外，DDPM的作者发现，省去损失函数中的加权项效果更好，

Ltsimple =Et∼[1,T],x0,ϵt[∥ϵt−ϵθ(xt,t)∥2]=Et∼[1,T],x0,,ϵt[∥ϵt−ϵθ(αˉtx0+1−αˉtϵt,t)∥2]\begin{aligned} L_t^{\text {simple }} & =\mathbb{E}_{t \sim[1, T], \mathbf{x}_0, \epsilon_t}\left[\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{t \sim[1, T], \mathbf{x}_{0,}, \epsilon_t}\left[\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right\|^2\right] \end{aligned}

最终的目标函数记为：

Lsimple=Ltsimple+CL_{simple} = L_{t}^{simple} + C

其中，CC是权重无关的常数。

5、小结

扩散模型DDPM的训练和采样算法如下图所示，

三、Extracting Training Data from Diffusion Models

论文地址：Extracting Training Data from Diffusion Models

这篇论文的意思就是扩散模型在近两年的表现牛逼上天了，但是它是不是就完美了呢？没有！他们发现扩散模型可以记住训练集中的样本，并在生成过程中进行复现。扩散模型容易受到记忆攻击，从而导致抄袭训练数据集的行为！

参考文献

[1] https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
[2] https://blog.csdn.net/Little_White_9/article/details/124435560
[3] https://www.bilibili.com/video/BV1b541197HX/?spm_id_from=333.1007.top_right_bar_window_default_collection.content.click&vd_source=7b8e971b43a022cac5ad76d689c0c177

EOF
👁📚31 posts