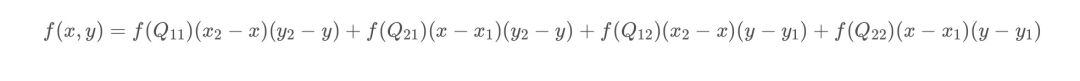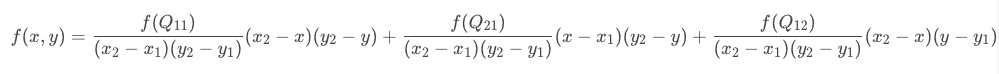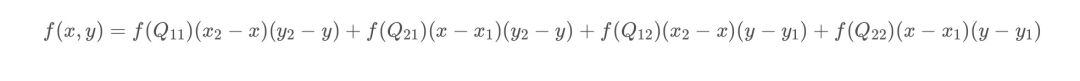chenjie04's blog

在学习可变形卷积的过程中，涉及到给采样点加上偏移量进行卷积感受野变形的操作，但是偏移量是浮点数，偏移后一般不能保证刚好落到某个像素点上，多是落到类似（10.3，25.7）这样的虚拟像素点上，这样我们就需要用到双线性插值法来计算出虚拟像素点的值。

双线性插值法就是找出虚拟像素点周围最近的4个真实像素点，然后对这4个像素点的值进行加权求和，作为虚拟像素的值。

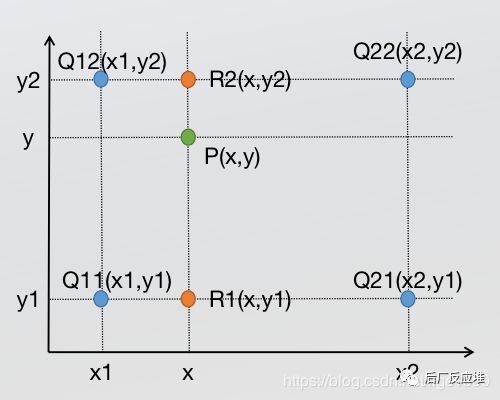
如上图所示（图片来自: https://zhuanlan.zhihu.com/p/110754637），假设我们的虚拟像素点为$P(x,y)$。首先，我们需要找出周围最近的4个真实像素点: $Q11(x1,y1)$、$Q12(x1,y2)$、$Q21(x2,y1)$、$Q22(x2,y2)$。怎么找？简单！$x$向下取整得到$x1$，$x1+1$得到$x2$；$y$向下取整得到$y1$，$y1+1$得到$y2$；支持4个点全部找到。

然后，$Q11(x1,y1)$和$Q21(x2,y1)$进行一个x方向的插值，求出点$R1$的值（记为$f(R1)$，其他点同理）。具体怎么做？我们说$R1$越靠近$Q11$，那么$f(Q11)$的权重就应该越大，反之越小。很直观，很合理吧？从图中，我们可以看到$R1$刚好把$(x2 - x1)$分成了$x2-x$和$x-x1$两段。$R1$越靠近$Q11$，段$x2-x$越长，$x-x1$越短，那么我们把$x2-x$/$x2 - x1$作为$f(Q11)$的权重不就好了吗？同样$x-x1$/$x2 - x1$作为$f(Q21)$的权重，则有：

$f(R1) = \frac{x2-x}{x2-x1} f(Q11) + \frac{x-x1}{x2-x1} f(Q21)$

同样，$Q12(x1,y2)$和$Q22(x2,y2)$进行一个x方向的插值，求出点$R2$的值:

$f(R2) = \frac{x2-x}{x2-x1} f(Q12) + \frac{x-x1}{x2-x1} f(Q21)$

最后，$R1(x,y1)$和$R2(x,y2)$进行一个y方向的插值，就求出点$P(x,y)$的值:

$f(P) = \frac{y2-y}{y2-y1} f(R1) + \frac{y-y1}{y2-y1} f(R2)$

把前面求得的$f(R1)$，$f(R2)$代进来得：

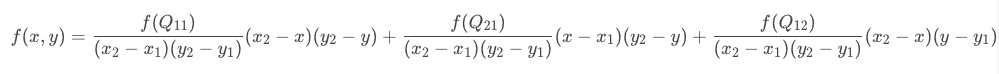
因为分母都为1，所以得