——根据台大李宏毅老师的《强化学习》课程笔记而来！

一、什么是强化学习

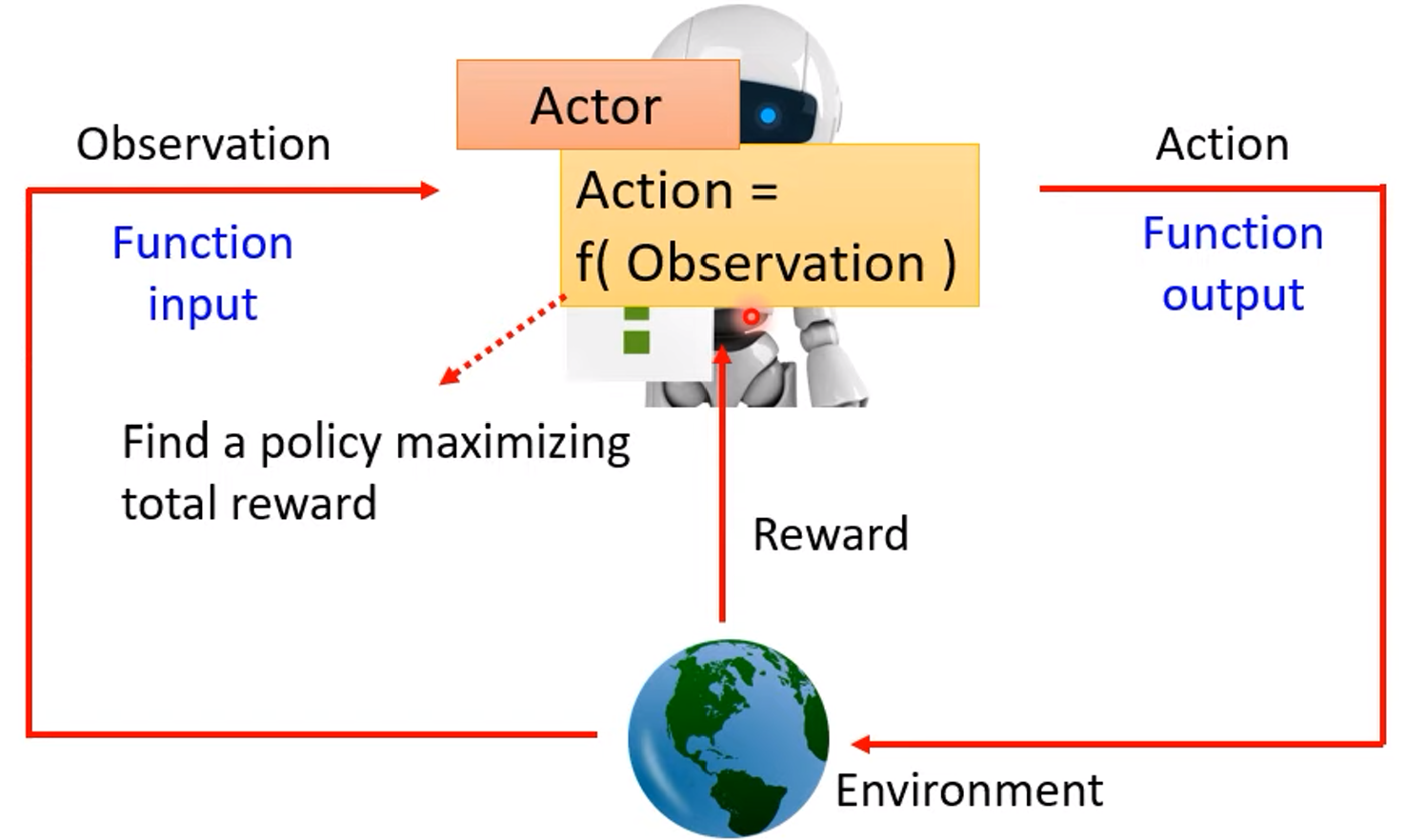
当我们谈论什么是强化学习时总会看到上面这张图：强化学习就是智能体（Actor）对环境进行观测，然后根据观测结果（Observation）采取相应的动作（Action），动作作用于环境（Environment）之后，环境就会产生相应的变化，这样智能体就可以再一次得到新的观测，同时环境也会给智能体一个反馈（Reward）表明这个动作是好的还是不好的。强化学习就是想办法找到一个策略能够最大化总的反馈（Total reward）。

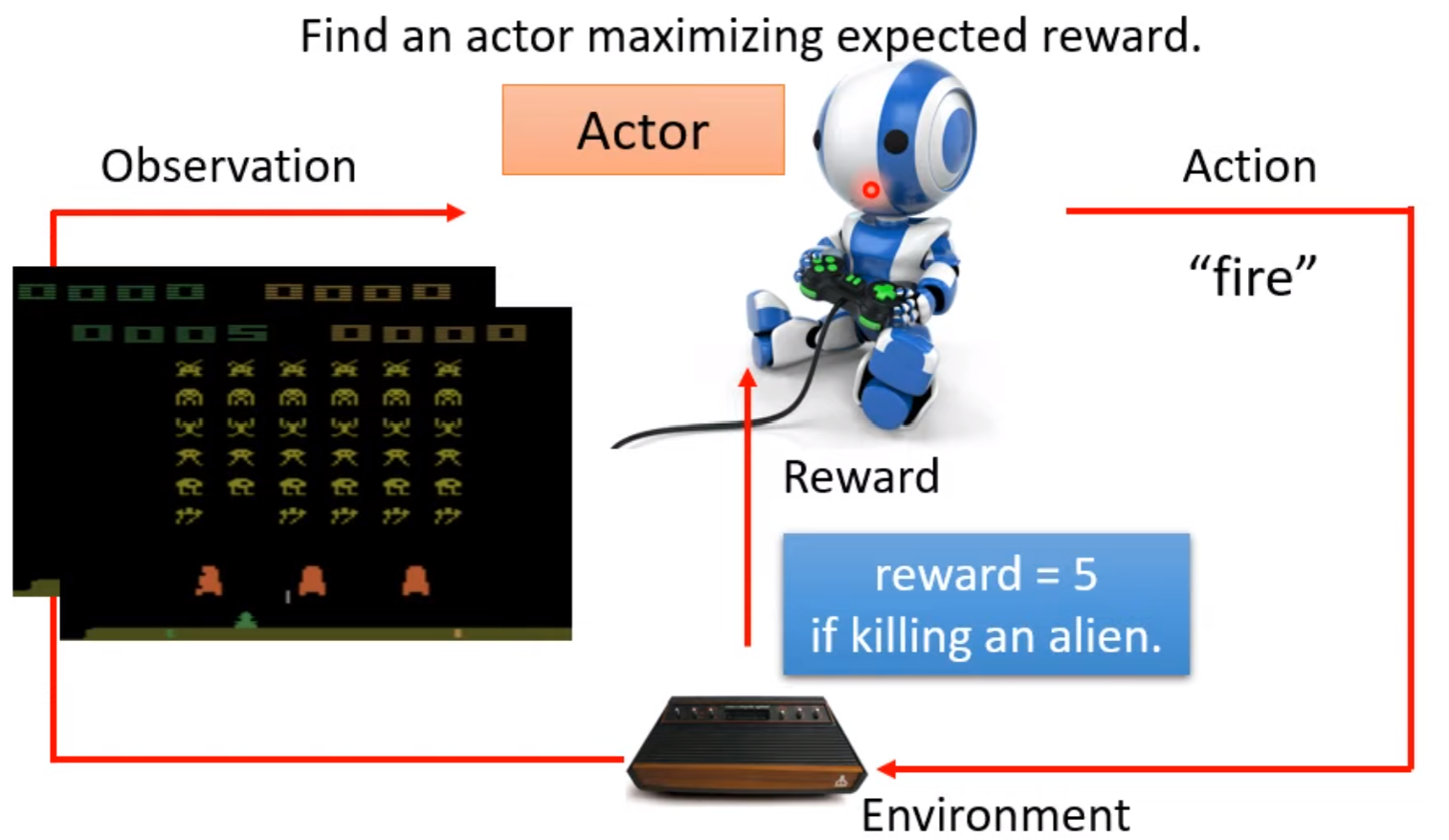
以一个打“Space Invader”小游戏的例子来进行说明，Actor去打小游戏，那么这里的环境就是游戏机，游戏的画面就是Actor可以观测到画面，Actor根据看到的画面控制己方太空梭左右移动或开火击杀小外星人，比如这里Actor采取的动作的开火，游戏机会根据Actor采取的动作给予反馈，比如这里左右移动没有分，而开火并击杀外星人得5分。那么这里强化学习就是训练Actor使他能够得到最高的分数。

上面这些是介绍强化学习都必然提到的基础知识，但是强化学习到底该怎么做呢？还是一头雾水啊！

二、怎么训练强化学习

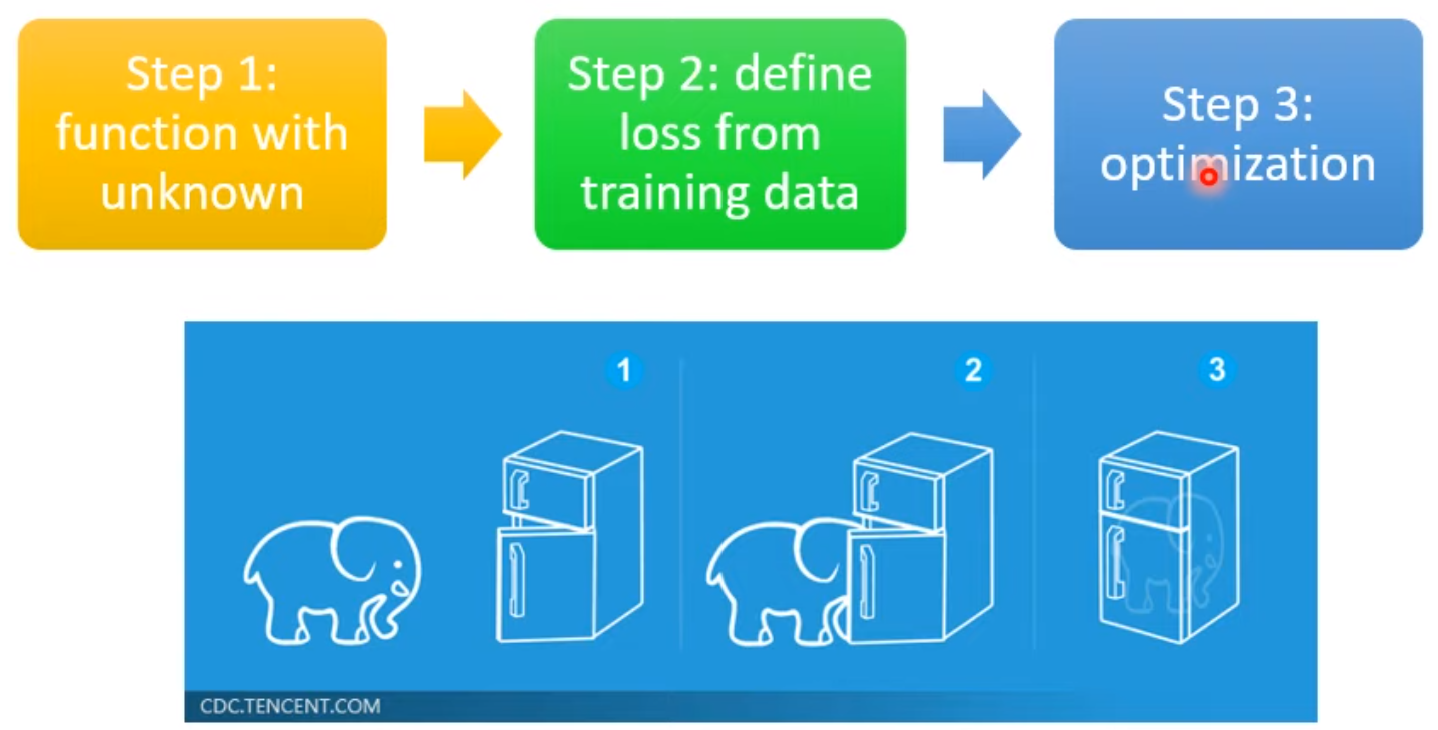
之前说过机器学习的三步走很简单：第一步是定义一个带有未知参数的函数（比如神经网络），然后根据训练数据设计损失函数，第三步就是优化。其实强化学习也一样。

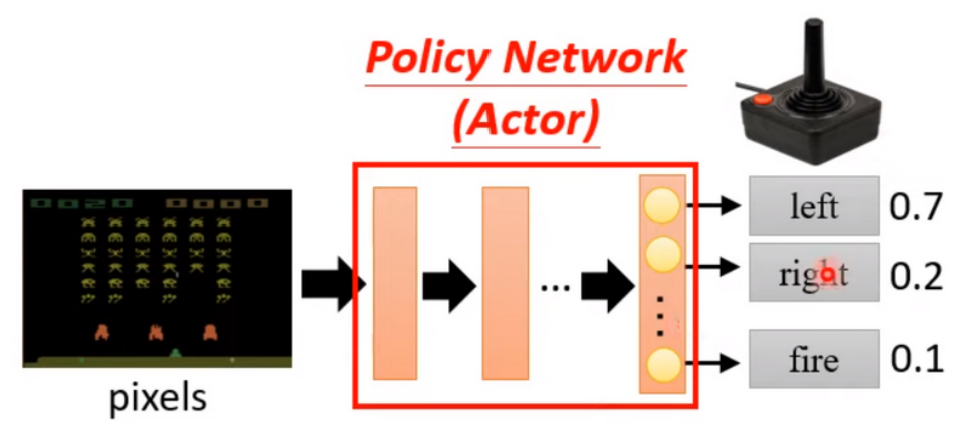
在强化学习里面，带有未知参数的函数就是我们的Actor或者交Policy Network，它的输入是游戏画面，输出的采取各个动作的概率。其实这跟我们的图像分类问题的一样的，输入图像，输出图像所属的类别，所以说我们甚至可以直接采用图像分类的网络架构。唯一不同的是在强化学习里面不是直接根据预测的概率选择动作，而是在这些动作里再做一次抽样。这一步在强化学习里面很重要，这叫Exploration，它可以增加Actor采取行动的随机性，这样可以探索一些以前没有考虑过的行为，从而增大习得最优策略的可能性。

那么我们怎么定义强化学习的损失函数呢？

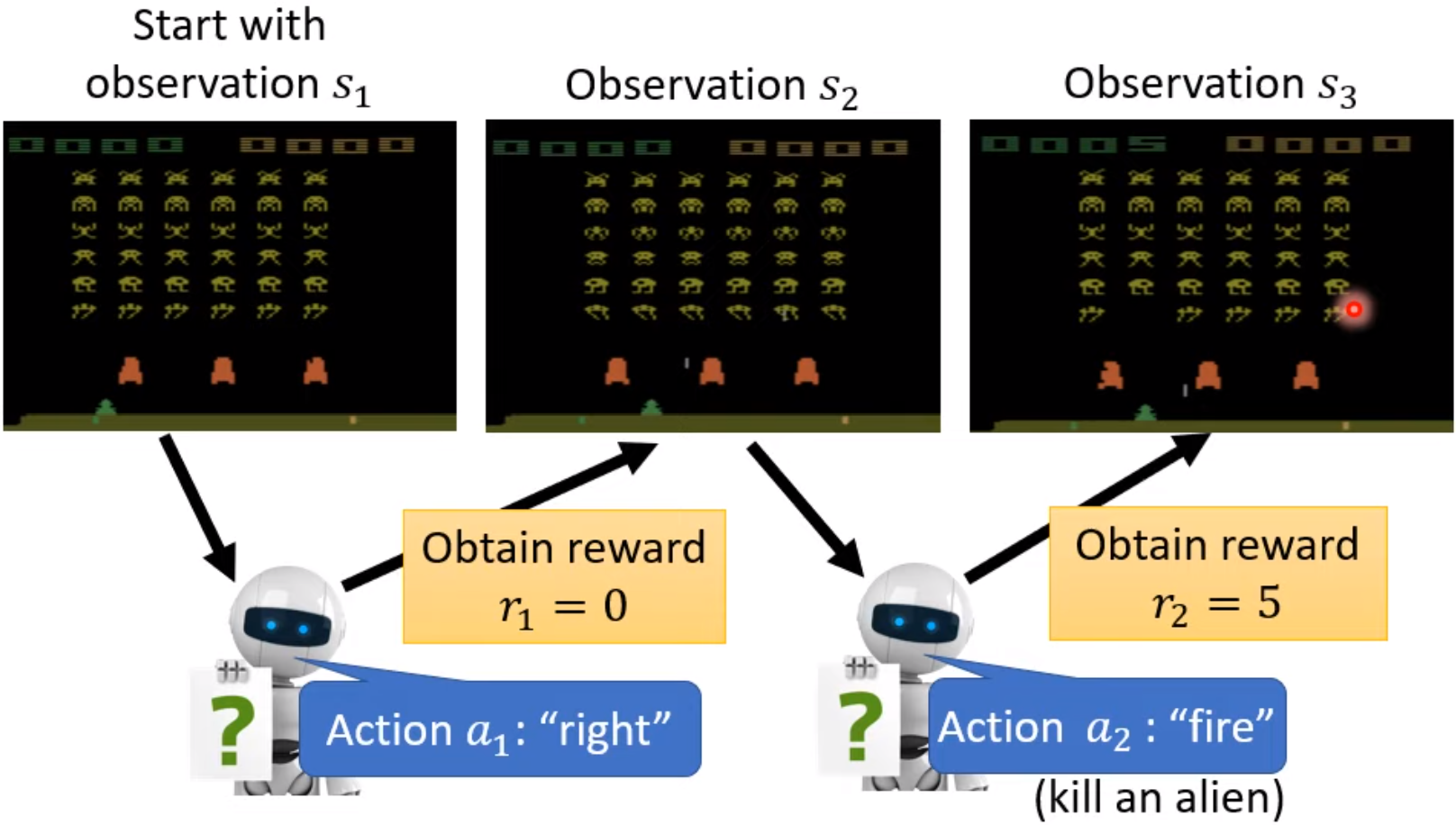
前面说过Actor观测到一个画面就会采取一个动作，同时环境会给它一个反馈 $r_{t}$ ，直到己方的太空梭被摧毁或者杀光外星人，游戏结束。游戏结束后，我们得到一个Total reward：$R = \sum^{T}_{t=1} r_{t}$，我们的任务就是要最大化Total reward，那么我们就可以把Total reward取负号当作我们的损失函数。

最后，强化学习该怎么优化？

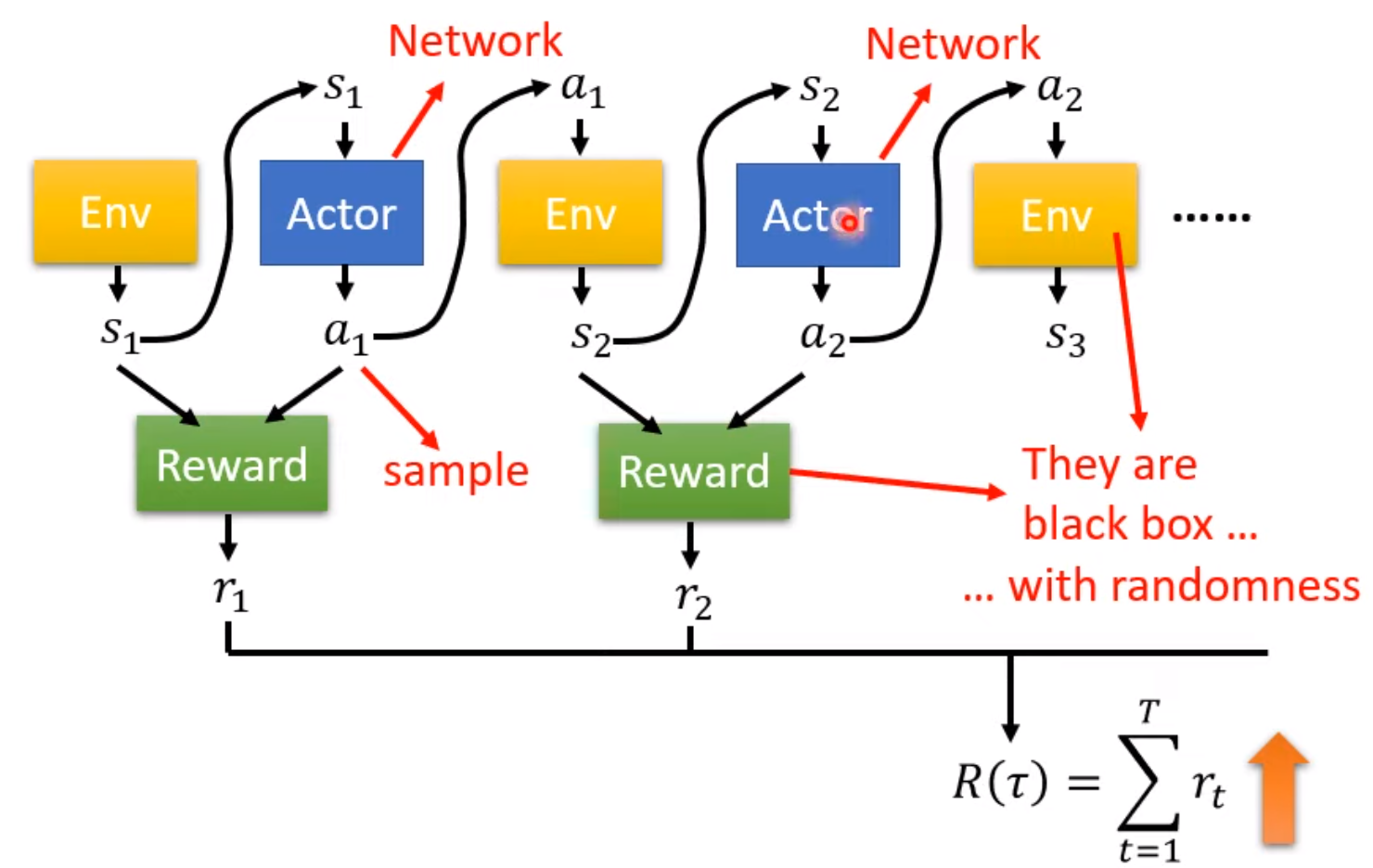
在讨论之前，我们先用另外一幅图示重新审视强化学习。如上图所示，首先Actor从环境环境中得到第一个观测$s_{1}$，根据$s_{1}$采取动作$a_{1}$, $a_{1}$作用于环境之后得到$s_{2}$，Actor根据$s_{2}$采取动作$a_{2}$，如此循环往复直到游戏结束，我们就得到了一条Trajectory $\tau = \{ s_{1}, a_{1}, s_{2}, a_{2}, ...\}$。然后，我们来看Reward，可以把Reward当作一个函数，判断Actor根据$s_{i}$采取动作$a_{i}$是否合理。当游戏结束，我们就可以得到Total reward。我们知道Actor是一个神经网络，其实如果环境和Reward都是神经网络的话，整个强化学习模型就像一个RNN，采用RNN的方法就可以解了。但是，问题在于环境和reward都是黑盒，而且带有一定的随机性，比如用强化学习下棋的时候，Actor下完一子之后，它的环境（也就是它的对手——人会采取哪一步是不确定的）。另外，Actor根据观测采取的动作也是具有随机性的，因为action是要随机抽样的。这两个问题让强化学习的训练十分困难，强化学习的核心也就在优化这一步。

接下来，我们将一步一步去接这个强化学习的优化问题。

首先，我们得研究怎么控制我们的Actor，让它在给定的观测时做或者不做指定的动作。

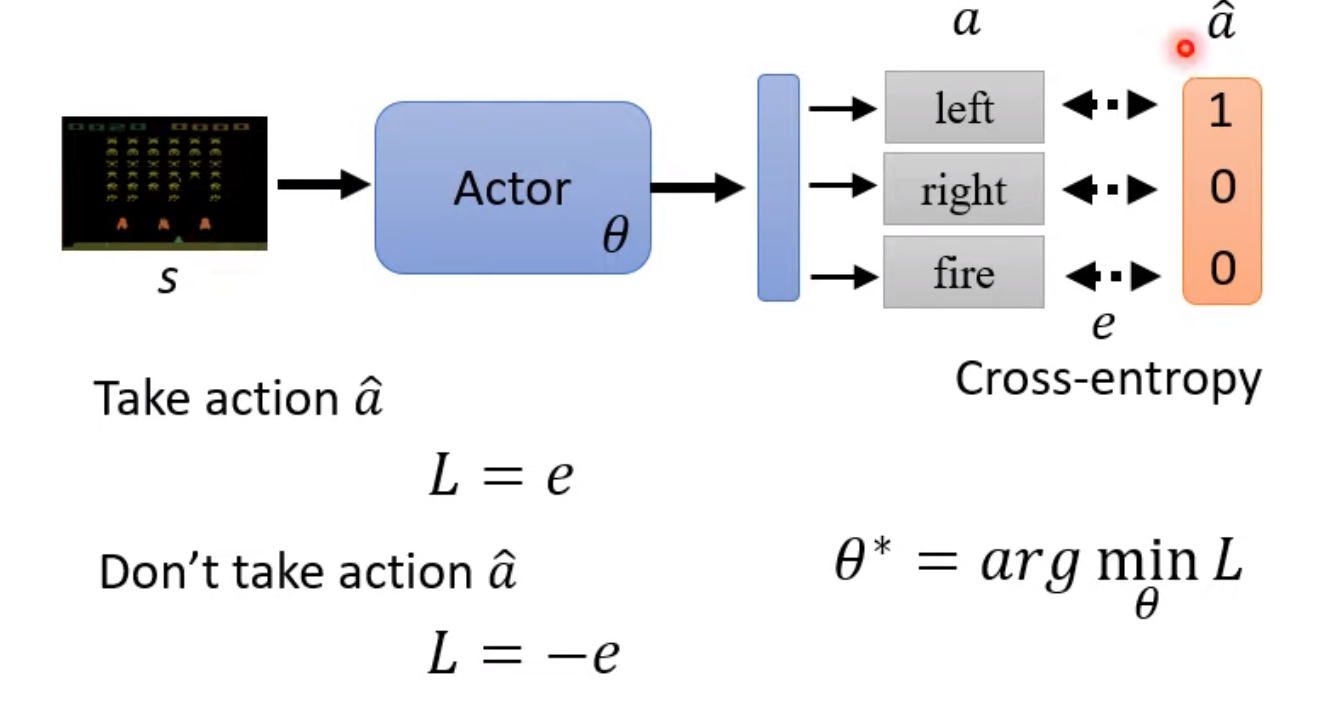
我们可以先把它想象成一个分类问题，假如我们知道给定观测应该采用的动作ground-truth，比如给定观测$s$应该采取的动作为$\hat{a}$，我们只需要计算Actor的输出$a$与$\hat{a}$的交叉熵并将它定义为Loss，那么找到一个参数$\theta$最小化Loss就可以让Actor采取特定的动作。那么我们又是怎么让Actor不要采取指定的动作呢？只需要将Loss定义为负的交叉熵即可。所以说我们是可以控制我们的Actor的，只要我们能够给予合适的标签数据。

所以，我们希望可以收集到这样的训练数据，指定在什么样的观测采取什么样的动作，在什么样的观测时不要采取什么动作，这样我们就可以根据训练数据来定义我们的Loss，最后通过最小化Loss来训练我们的强化学习。

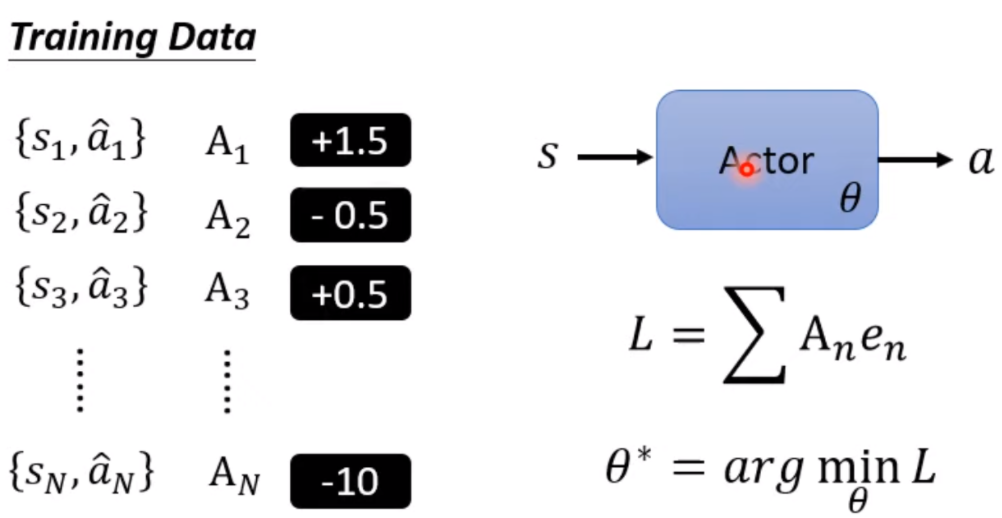
甚至，我们进一步制定每个动作的重要程度，比如$s_{1}$时比较希望采取动作$a_{1}$，但是在$s_{N}$时绝对不要采取动作$a_{N}$, 此时，我们的Loss就变成了$L=\sum A_{n}e_{n}$。

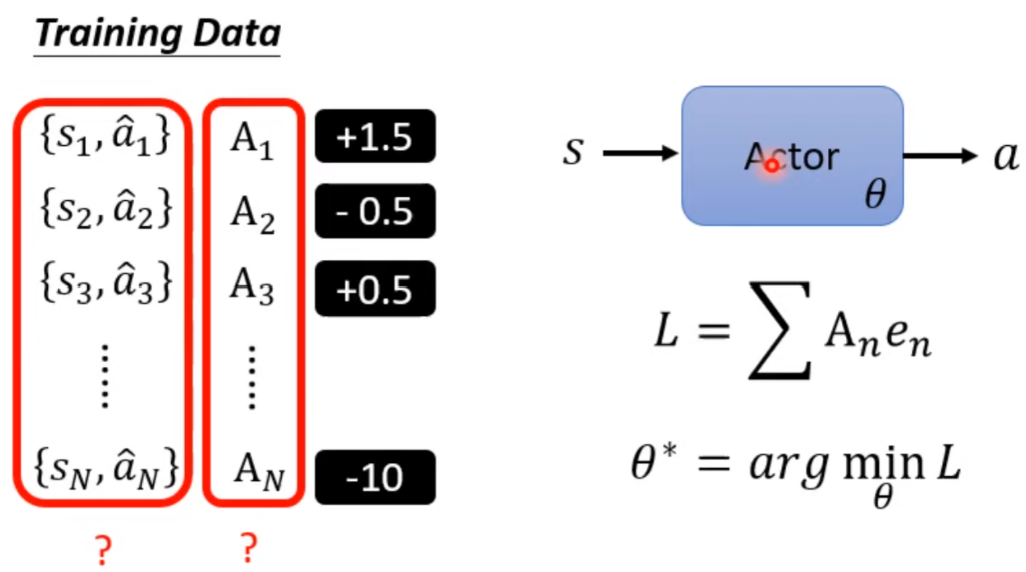
接下来，我们的重点就是怎么去收集这样的训练数据和怎么定义每个动作的重要程度$A_{n}$。

Version 0

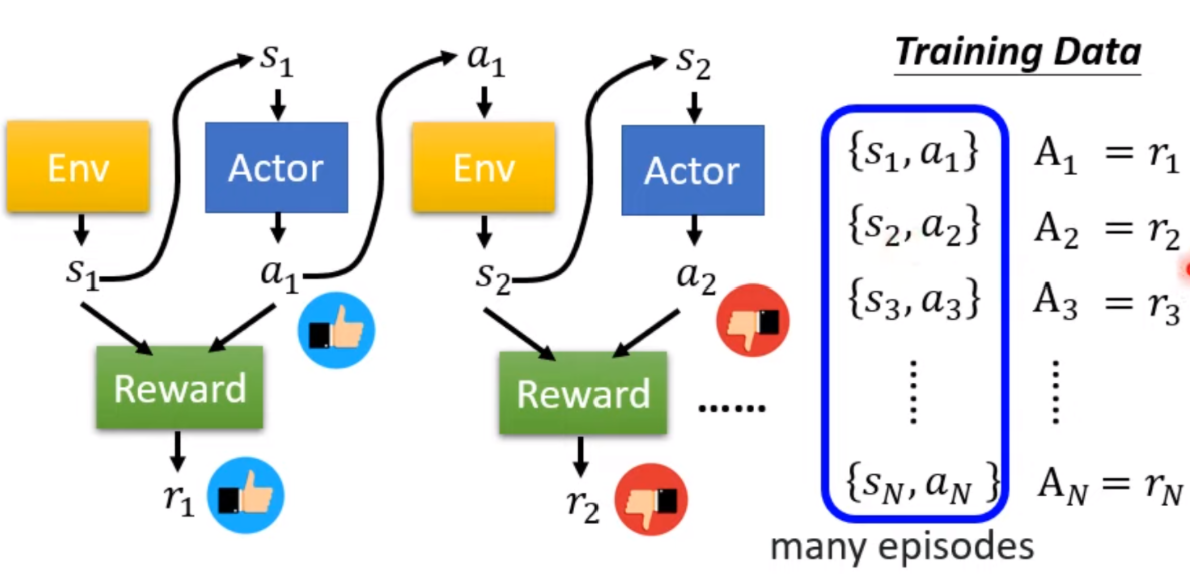
Version 0 是一个简单单不正确的版本，我们就先随机初始化一个Actor，然后就让它去玩几把游戏，然后把$\{(s_{i},a_{i})\ | \ i=1...N\}$ 记录下来就得到了训练数据。另外，在玩游戏的过程中，Actor每采取一个动作就可以得到一个reward，我们把每次的reward都记录下来作为评价action重要程度的指标，这样我们就可以训练强化学习了。

但是这样训练出来的Actor是一个短视的Actor，急功近利！比如在space invader游戏里面，左右移动都没有得分，只有开火并击杀外星人才会得分，这样训练出来的Actor，可能就是一个只会盲目开火的废材，因为我们知道有时候我们需要左右移动进行瞄准才会射击得准。换句话说动作$a_{1}$会影响动作$a_{2}$的得分，$a_{2}$会影响$a_{3}$，以此类推，它们是相互关联的，而不是独立的。为了解决Actor这种短视的问题，我们引入Version 1.

Version 1

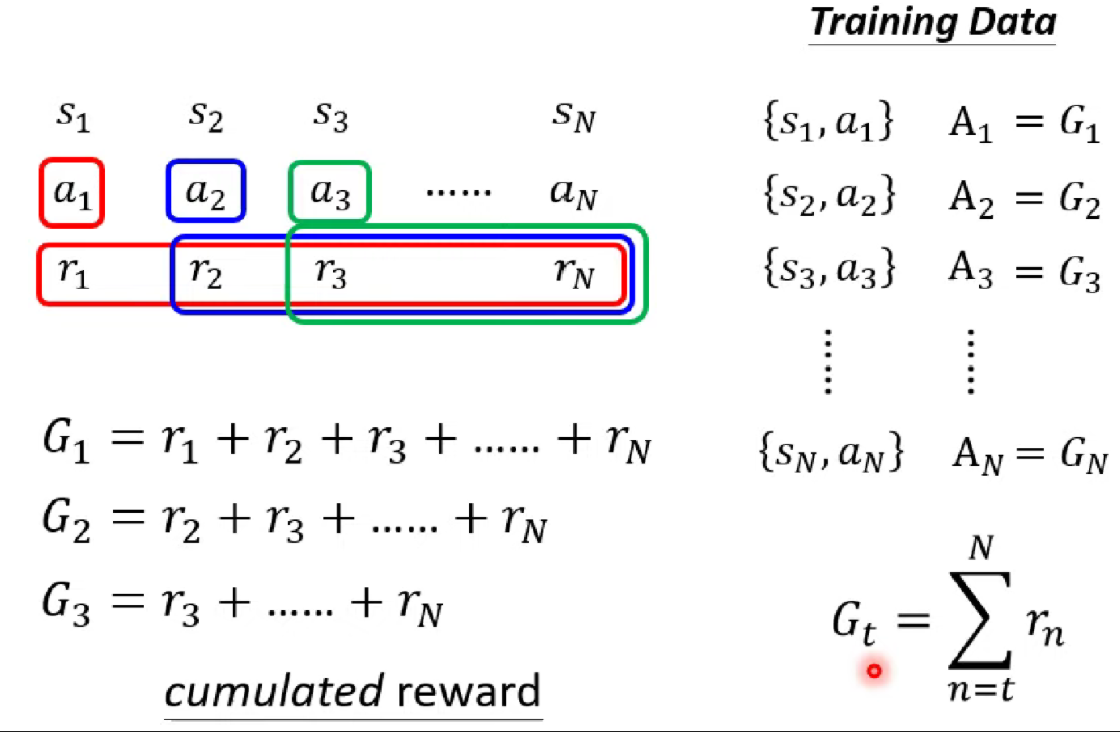
在Version 1中，我们不是将每个动作的reward作为评判重要性的指标，而是将当前reward以及往后直到游戏结束的所有reward加起来得到累积奖励，把这个累积奖励作为评判重要性的指标。这样的话，我们的Actor可能就学会做一个长期规划，学会放弃短期利益来获取长期更大的收益。但是，version 1也存在问题，那就是当游戏很长的时候，你说$a_{1}$会影响到$a_{3}$的reward我信，但是你说$r_{N}$也是$a_{1}$的功劳，那就不太可能了。换句话说就是当前动作可能会对后续动作产生影响，但是这个影响不可能是无穷的。因此，我们迎来了Version 2.

Version 2

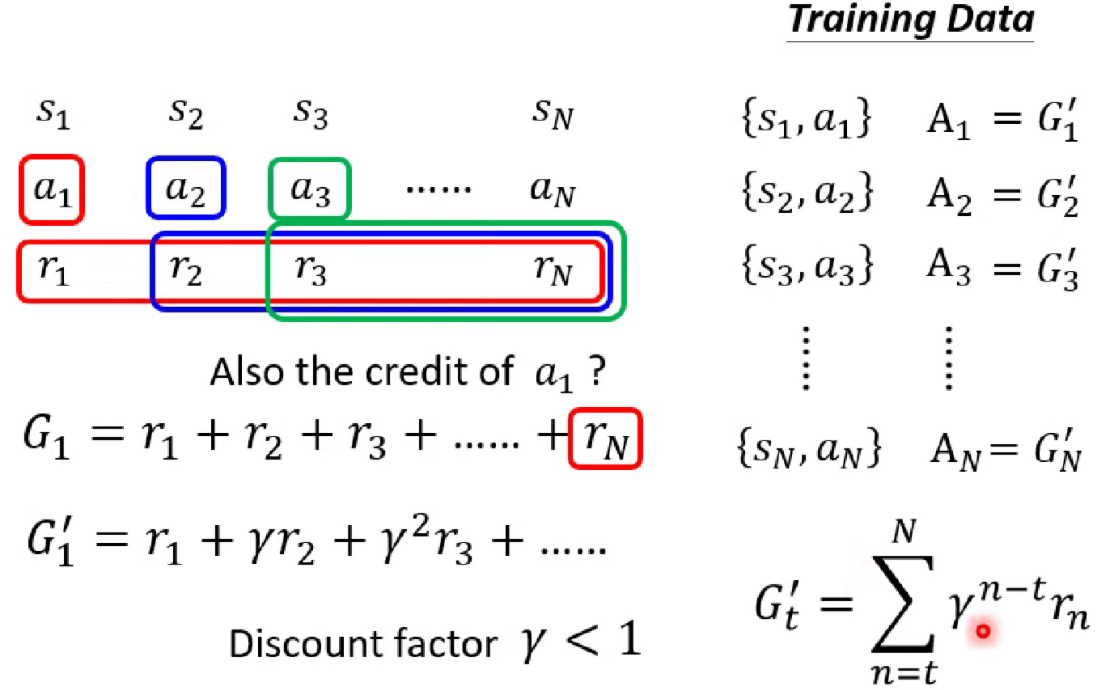
Version 2中主要是引入一个衰减因子 $\gamma<1$，如上图所示，衰减累积奖励记为$G^{'}_{t}=\sum^{N}_{n=t}\gamma^{n-t}r_{n}$，这样离得越远影响就越小，合情合理（从此之后为了不拗口，衰减累积奖励都简称为累积奖励）。但是这就完美了吗？其实并没有。我们知道动作有好有坏，所以$A_{N}$应该有正有负，但是比如在space invader里面，左右移动得0分，击杀外星人得5分，那么它的衰减累积奖励就全都是正的啊。为了解决这个问题，我们就来到了version 3.

Version 3

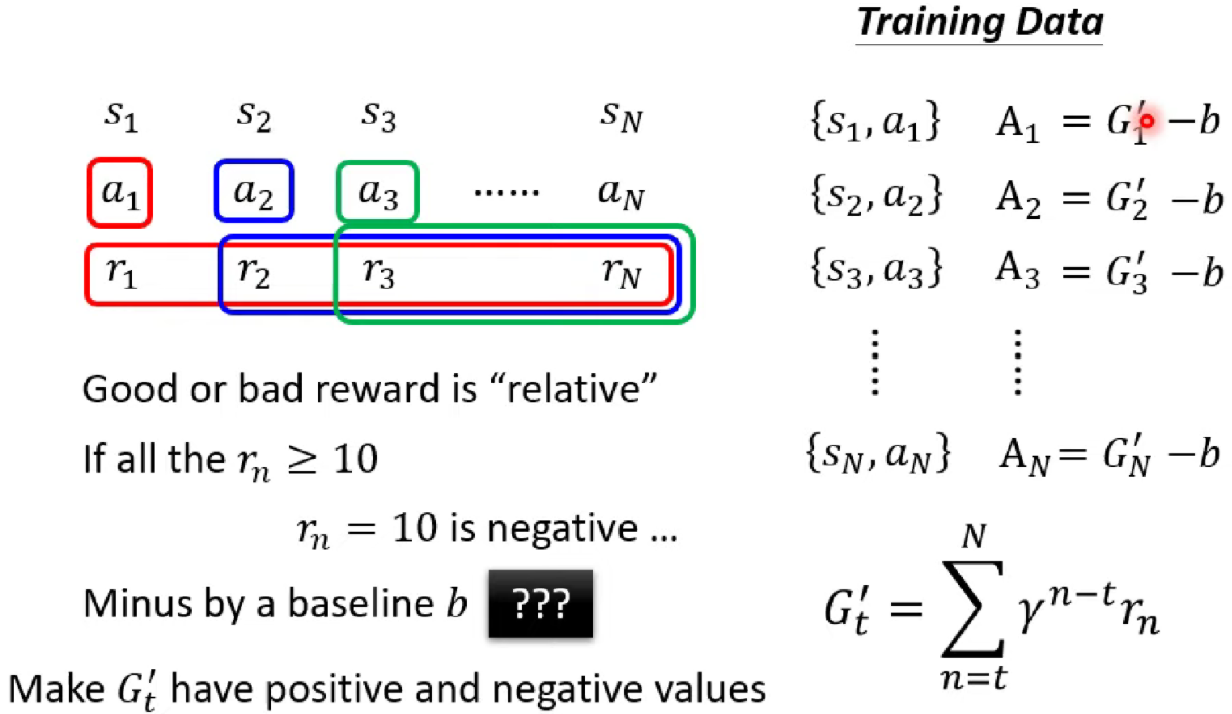
在version 3中考虑的问题是这样，对于那些衰减累积奖励全是正的问题，一个行为的好坏是相对的，比如$r_{n}=10$，看起来它可能是好的，但是如果所有其他$r_{n}\ge 10$，那么$r_{n}=10$就是不好的。所以说version 3就是在衰减累积奖励的基础上减去一个baseline，衰减累积奖励让累积奖励有正有负，从而更好地判断一个动作是好的还是不好的。这个版本就是我们熟知的Policy Gradient.

Policy Gradient

接下来，我们就总结一下Policy Gradient这个方法是怎么做的。首先就是初始化actor为$\theta ^{0}$，然后进入迭代训练，在每次迭代中，首先让之前的actor $\theta ^{i-1}$ 与环境进行交互，然后收集训练数据$\tau=\{(s_{1},a_1),(s_2,a_2),...,(s_N,a_N)\}$, 然后计算$\{A_1,A_2,...,A_N\}$，计算Loss，最后采用梯度下降更新actor。

曾经，我有个疑问：为什么在policy gradient中是计算所有训练数据的loss再更新actor网络，即收集一遍数据只能更新actor一次，而不是采用深度学习里面的mini-batch的训练方式。一个比较合理的解释是“吾之蜜糖，彼之砒霜”，这里的训练数据是用$\theta ^{i-1}$收集的，一旦你中间对$\theta ^{i-1}$更新了，那么可能剩下的数据可能就不适用于训练$\theta ^{i-1}$了。

但是其实这个问题就见仁见智了。

On-policy v.s Off-policy

其实，像上面这种被训练的Actor和拿去跟环境交互的Actor是同一个的情形，被称为on-policy。On-policy的强化学习最好就是收集一次数据更新一次模型。但是，我们人类可以根据别人的经验学习啊，看着别人去做一件事情，我们也可以学会啊！这种被训练的Actor和拿去跟环境交互的Actor不同的情形，被称为off-policy。Off-policy的优势在于采取特定手段我们就可以收集一次数据更新很多次模型。其中，一个典型的off-policy算法就是 Proximal Policy Optimization (PPO)。

Proximal Policy Optimization (PPO)

PPO这个方法它之所以能够从on-policy转到off-policy，主要是基于importance sampling。

Importance sampling

假设 $x$ 服从未知分布 $p(x)$ , 如果我们要求 $f(x)$ 的期望 $E_{x \sim p}[f(x)]$，那么我们可以从$p(x)$ 中抽样一堆数据$x^i$，然后通过求均值来近似$f(x)$ 的期望，即

$E_{x \sim p}[f(x)] \approx \frac{1}{N} \sum^{N}_{i=1}f(x^i)$

但是有时候我们却无法从$p(x)$ 中抽样，只能在$q(x)$中抽样。就好像现在我们只有$\theta ^{i-1}$收集到的数据，却没有$\theta^i$收集的数据，$\theta ^{i-1}$收集到的数据只能用于更新$\theta^{i-1}$，不能用来更新$\theta^i$。off-policy想要达到的目的就是希望可以利用$\theta ^{i-1}$收集到的数据多次更新$θ^i$,从而提高效率。回到我们的importance sampling中，现在我们就是希望可以利用部分$q(x)$中抽样到的数据来计算$f(x)$ 的期望$ E_{x \sim p}[f(x)]$。

我们将$E_{x \sim p}[f(x)]$写成积分的形式，然后上下同乘$q(x)$，然后就可以写成从$q(x)$里面抽样的数据来求期望。

$\begin{aligned} E_{x \sim p} [f(x)] =& \int f(x)p(x)dx \\ =& \int f(x) \frac{p(x)}{q(x)} q(x) dx \\ =& E_{x\sim q}[f(x) \frac{p(x)}{q(x)}] \end{aligned}$

从上面的式子，我们知道其实我们是可以通过一个权重$\frac{p(x)}{q(x)}$修正两个分布之间的差异。当然，分布$p(x)$和$q(x)$不能差异太大。这就是importancesampling。

我们回顾一下，policy gradient的目的是最大化期望的reward，根据version 3的说法可以写成$E_{(s_t,a_t) \sim \pi_{\theta^{i}}}[A^{\theta^{i}}(s_t,a_t)]$，根据公式$\nabla f(x) = f(x) \nabla log f(x)$,梯度可以写为

$=E_{(s_t,a_t) \sim \pi_{\theta^{i}}} [A^{\theta^{i}}(s_t,a_t) \nabla logp_{\theta^{i}} (a_t^n | s_t^n)]$

但是我们现在只有从$\theta^{i-1}$的数据，根据importance sampling，

$=E_{(s_t,a_t) \sim \pi_{\theta^{i-1}}} [\frac{p_{\theta^ {i}}(s_t,a_t)}{p_{\theta^ {i-1}}(s_t,a_t)} A^{\theta^{i}}(s_t,a_t) \nabla logp_{\theta^{i}} (a_t^n | s_t^n)]$

因为数据是从$\theta^{i-1}$采样的，所以

$=E_{(s_t,a_t) \sim \pi_{\theta^{i-1}}} [\frac{p_{\theta^ {i}}(s_t,a_t)}{p_{\theta^ {i-1}}(s_t,a_t)} A^{\theta^{i-1}}(s_t,a_t) \nabla logp_{\theta^{i}} (a_t^n | s_t^n)]$

将联合概率分布改写成条件概率分布

$=E_{(s_t,a_t) \sim \pi_{\theta^{i-1}}} [\frac{p_{\theta^ {i}}(a_t|s_t)}{p_{\theta^ {i-1}}(a_t|s_t)} \frac{p_{\theta^ {i}}(s_t)}{p_{\theta^ {i-1}}(s_t)} A^{\theta^{i-1}}(s_t,a_t) \nabla logp_{\theta^{i}} (a_t^n | s_t^n)]$

其中，因为我们的actor是神经网络，我们可以直接把$s_t$输入，就得到$a_t$的条件概率，因此$\frac{p_{\theta^ {i-1}}(a_t|s_t)}{p_{\theta^ {i}}(a_t|s_t)}$很容易求。但是另外一项$\frac{p_{\theta^ {i-1}}(s_t)}{p_{\theta^ {i}}(s_t)}$不知道该怎么求，所以我们说服自己每次玩游戏观测到特定画面的概率是一样的，所以这一项不重要，我们把它去掉，那么我们就得到

$=E_{(s_t,a_t) \sim \pi_{\theta^{i-1}}} [\frac{p_{\theta^ {i}}(a_t|s_t)}{p_{\theta^ {i-1}}(a_t|s_t)} A^{\theta^{i-1}}(s_t,a_t) \nabla logp_{\theta^{i}} (a_t^n | s_t^n)]$

相应的，我们的目标函数就是最大化期望累积奖励，

$J^{\theta^{i-1}}(\theta^i)=E_{(s_t,a_t) \sim \pi_{\theta^{i-1}}} [\frac{p_{\theta^ {i}}(a_t|s_t)}{p_{\theta^ {i-1}}(a_t|s_t)} A^{\theta^{i-1}}(s_t,a_t)]$

$J^{\theta^{i-1}}(\theta^i)$中$J$的上标表示从$\theta^{i-1}$收集的数据，更新的是$\theta^{i}$的参数。

所以说PPO的核心是更新参数的那个actor必须要有意识知道自己和跟环境互动的那个actor是不一样的，为了做区别，我们把目标函数写成

$J^{\theta^{'}}(\theta)=E_{(s_t,a_t) \sim \pi_{\theta^{'}}} [\frac{p_\theta (a_t|s_t)}{p_{\theta^ {'}}(a_t|s_t)} A^{\theta^{'}}(s_t,a_t)]$

拿$\theta^{'}$收集的数据去更新$\theta$。

前面我们讲importance sampling的时候说过，两个分布不能相差得太多，相差太多得到的结果就不可能好。那么，在PPO里就是更新参数的actor和跟环境互动的actor不能差距过大，所以PPO就在目标函数加一个$KL$散度正则化项，

$J^{\theta^{'}}_{PPO}(\theta)=E_{(s_t,a_t) \sim \pi_{\theta^{'}}} [\frac{p_\theta (a_t|s_t)}{p_{\theta^ {'}}(a_t|s_t)} A^{\theta^{'}}(s_t,a_t)] -\beta KL(\theta,\theta^{'})$

需要注意的是，$KL$散度不是对actor的参数做限制，而是对actor的行为（即actor的输出）做限制。

现在，我们对PPO做一个总结：

首先，初始化策略参数为$\theta^0$，然后开始迭代训练，在每一次迭代中，用$\theta^k$去跟环境交互，收集数据$\{s_t,a_t\}$，计算$A^{\theta^{k}}(s_t,a_t)$，然后根据目标函数优化模型。这里需要注意的是PPO的参数可以更新很多次，充分提高了数据利用效率。最后，还对$\beta$做自适应调整，控制更新参数的actor和跟环境互动的actor不会差距过大。

PPO还有另外一个比较容易实现的版本：

$J^{\theta^{k}}_{PPO2}(\theta) \approx \sum_{(s_t,a_t)} (\frac{p_\theta (a_t|s_t)}{p_{\theta^ {k}}(a_t|s_t)} A^{\theta^{k}}(s_t,a_t), clip(\frac{p_\theta (a_t|s_t)}{p_{\theta^ {k}}(a_t|s_t)}, 1-\varepsilon,1+\varepsilon) A^{\theta^{k}}(s_t,a_t) )$

主要是不用处理$KL$散度，比较容易实现，具体就不展开讲了，毕竟现在是入门。

Policy-based v.s. Value-based

前面讲的都是怎么训练一个actor，怎么更新actor采用的策略，所以它们是policy-based的方法。现在，我们讲的是另外一个东西叫critic，意为评估者，给定actor $\theta$ ，critic评估actor观测到状态$s$（并采用动作$a$）究竟好不好，或者说评估actor观测到状态$s$之后有可能得到多少的累积奖励。评判好不好，就是评判其价值，所以critic也叫value function（value function在深度强化学习里面也是神经网络）。

我们设critic为$V^\theta (s)$，表示评估actor $\theta$ 看到状态$s$之后有可能得到的累积奖励。

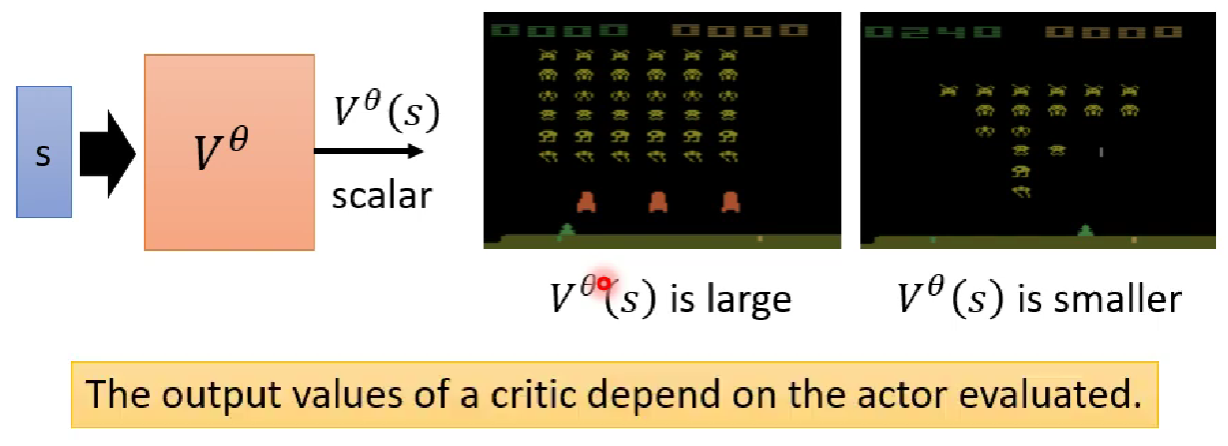
需要强调的是，critic是跟actor绑定的。例如上面的例子，如果是一个很优秀的actor，那么critic看到第一个画面有很多外星人可以杀，那么$V^\theta (s)$就会很大，看到第二个画面的时候外星人已经没多少了，所以$V^\theta (s)$就会变小。但是，如果是一个很烂的actor，不管看到什么画面，反正它都杀不了外星人，所以$V^\theta (s)$就会很小。

那么actor $\theta$看到状态$s$之后有可能得到的累积奖励是多少呢？我们当然可以等到游戏结束之后去把奖励都加起来，但是critic的目的就是要学会预测累积奖励！

怎么训练critic？

基于 Monte-Carlo（MC） 的方法

利用MC训练critic的方法很直接，你就拿actor去跟环境互动，然后收集数据，直接就可以拿收集到的数据去训练critic。比如，在一次互动中，我们看到状态$s_a$，当游戏结束得到了累积奖励为$G^{'}_{a}$，那么我们就得到了一笔训练数据，然后把$s_a$输入critic输出预测$V^{\theta}(s_a)$，接着跟ground-truth比较，计算loss，梯度下降训练。同样，当我们观测到状态$s_b$和对应的累积奖励$G^{'}_{b}$就又得到另外一笔训练数据。

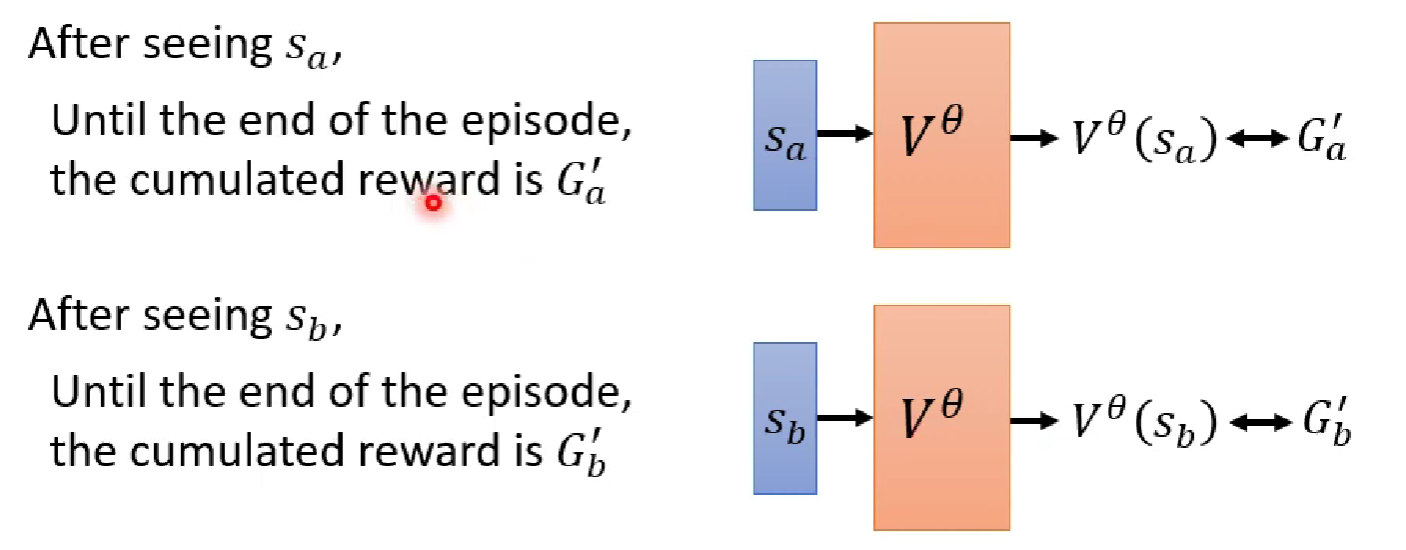
基于 Temporal-difference（TD） 的方法

在MC的方法中，我们是只有玩完整场游戏才能收集训练数据。TD希望了是观测到$...s_t,a_t,r_t,s_{t+1}...$ （即在观测到状态$s_t$，然后actor采取动作$a_t$，得到奖励$r_t$，状态进去$s_{t+1}$），这样的序列就可以训练critic。

我们来分析一下，

$V^{\theta}(s_t)=r_t+\gamma r_{t+1}+\gamma^{2}r_{t+2}+...\\ V^{\theta}(s_{t+1})=r_{t+1}+\gamma r_{t+2}+...$

那么，$V^{\theta}(s_t)=\gamma V^{\theta}(s_{t+1})+r_t$，这就是Temporal-difference。在训练的时候，将$s_t$和$s_{t+1}$分布输入$V^\theta$得到输出$V^{\theta}(s_t)$和 $V^{\theta}(s_{t+1})$，最后计算$V^{\theta}(s_t)-\gamma V^{\theta}(s_{t+1})$ 使它跟$r_t$越相近越好，这就是TD的训练过程。

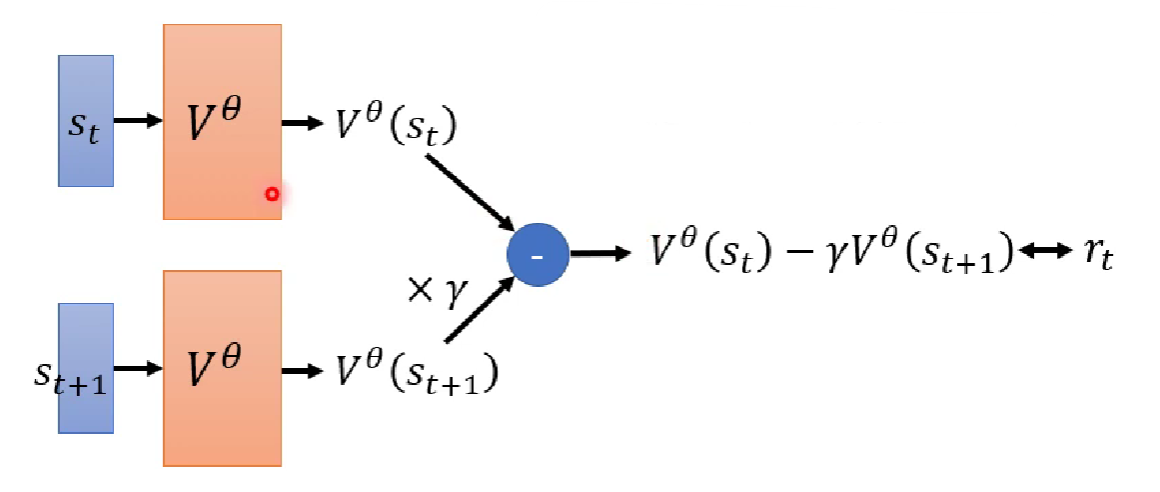
MC v.s. TD

MC和TD都可以用来训练我们critic，但是有时候用这两种方法计算出来的结果却不一样，因为我们观测到的数据指数部分数据而已，结果的不同是抽样导致的。一个简单的例子，假设我们玩了这个简单的小游戏8回，收集的数据如下，我们计算一下，$V^{\theta}(s_b)=3/4$这个很简单，没有问题。但是$V^{\theta}(s_a)$等于多少呢？根据MC的方法，我们只观测到一次$s_a$且它的累积奖励为$0$，那么$V^{\theta}(s_a)=0$；但是根据TD的方法，$V^{\theta}(s_a)=V^{\theta}(s_b)+r=3/4+0=3/4$。

上面讲的critic是评估actor $\theta $看到状态$s$之后有可能得到的累积奖励，所以也叫state value function。现在我们来看另外一个critic $Q^{\pi}(s,a)$，意思是actor $\theta$ 在看到状态$s$之后强制采取动作$a$有可能得到的累积奖励，也叫state-action value function或者$Q $ function。

$Q$ function把状态$s$和动作$a$作为输入，输出对应的预测累积奖励。

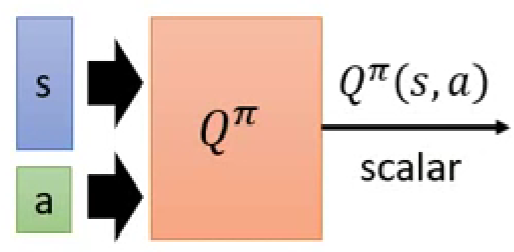
但是，对于动作action是离散的问题，我们通常可以将$Q$ function写成下面的形式，输入的是状态$s$，输出的不同action对应的累积奖励。

Critic的应用

我们学习出critic之后，critic该怎么用呢？第一个例子就是Q-learning。

Q-learning

Q-learning就是让actor $\pi$ 跟环境互动，然后通过TD或MC的方法来学出Q function $Q^{\pi}(s,a)$, 其实actor $\pi$ 就是根据Q function $Q^{\pi}(s,a)$的输出来选择动作，选择能最大化累积奖励的动作 $a$

$\pi ^{'}(s) = arg\ \underset{a}{max}\ Q^{\pi}(s,a)$

Q-learning在实践中会用到的技巧

1、Target network

第一个会用到的技巧的target network，它设置两个如下图所示的Q function，先固定住其中一个作为target network，然后采用TD的方式进行训练。把$s_t$和$a_t$输入Q function中，预测对应的累积奖励$Q^\pi (s_t,a_t)$, 把$s_{t+1}$和$\pi (s_{t+1})$输入到target network中预测对应的$Q^\pi (s_{t+1},\pi (s_{t+1}))$，根据TD的定义，这两者之间应该相差一个$r_t$，然后通过梯度下降最小化$Q^\pi (s_t,a_t)$和$r_t+Q^\pi (s_{t+1},\pi (s_{t+1}))$进行训练。

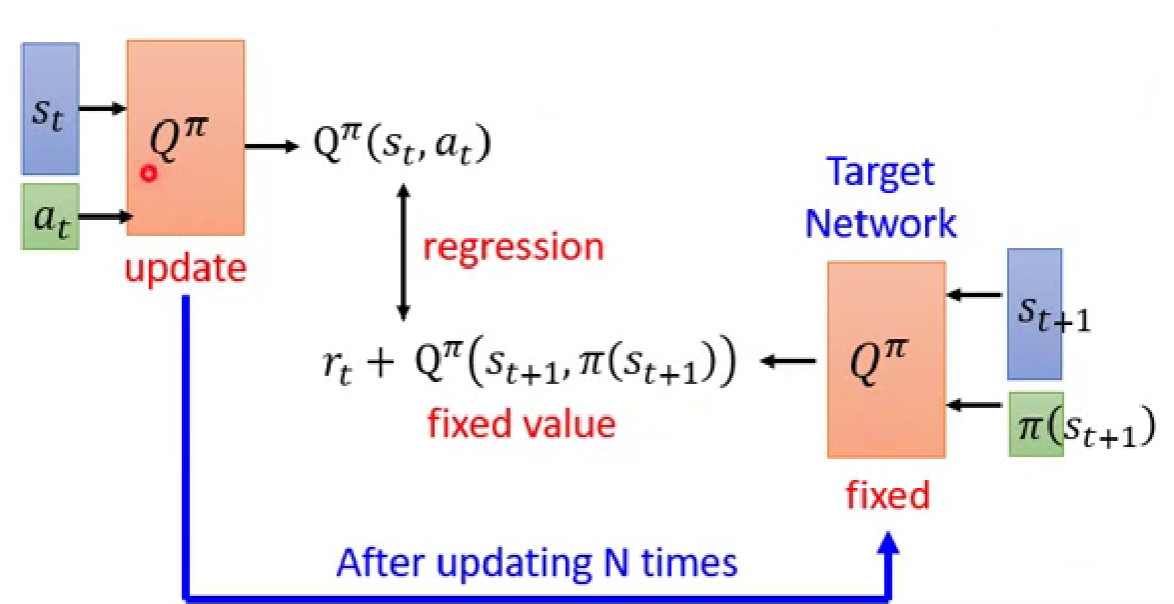
2、Exploration

前面说Q learning是选择能够最大化期望累积奖励的动作，其实这样不太好，我们讲过强化学习是需要进行探索的，所以说Q learning也要引入exploration。

Q learning的exploration通常可以有 Epsilon Greedy，将动作选取的规则定义为

$a = \left\{ \begin{aligned} &arg\ \underset{a}{max}\ Q^{\pi}(s,a),\ \ \ with\ probability\ 1-\varepsilon \\ &random, \ \ \ otherwise \end{aligned} \right.$

$\varepsilon$ 随着训练递减，因为在训练刚开始时需要更多地探索未知，当策略成熟之后，就应该更多地依赖策略做决策。

exploration也可以采用Boltzmann Exploration，计算每个动作的条件概率，

$p(a|s) = \frac{exp(Q(s,a))}{\sum_{a} exp((s,a))}$

可以选取概率比较高的动作。

3. Replay Buffer

Replay buffer就是将训练数据存到缓冲区，这里的每笔数据都是$(s_t,a_t,r_t,s_{t+1})$的形式，而且可以是来自不同的策略$\pi$的数据，训练的时候就从缓冲区中选取一个批次的数据来更新Q function。

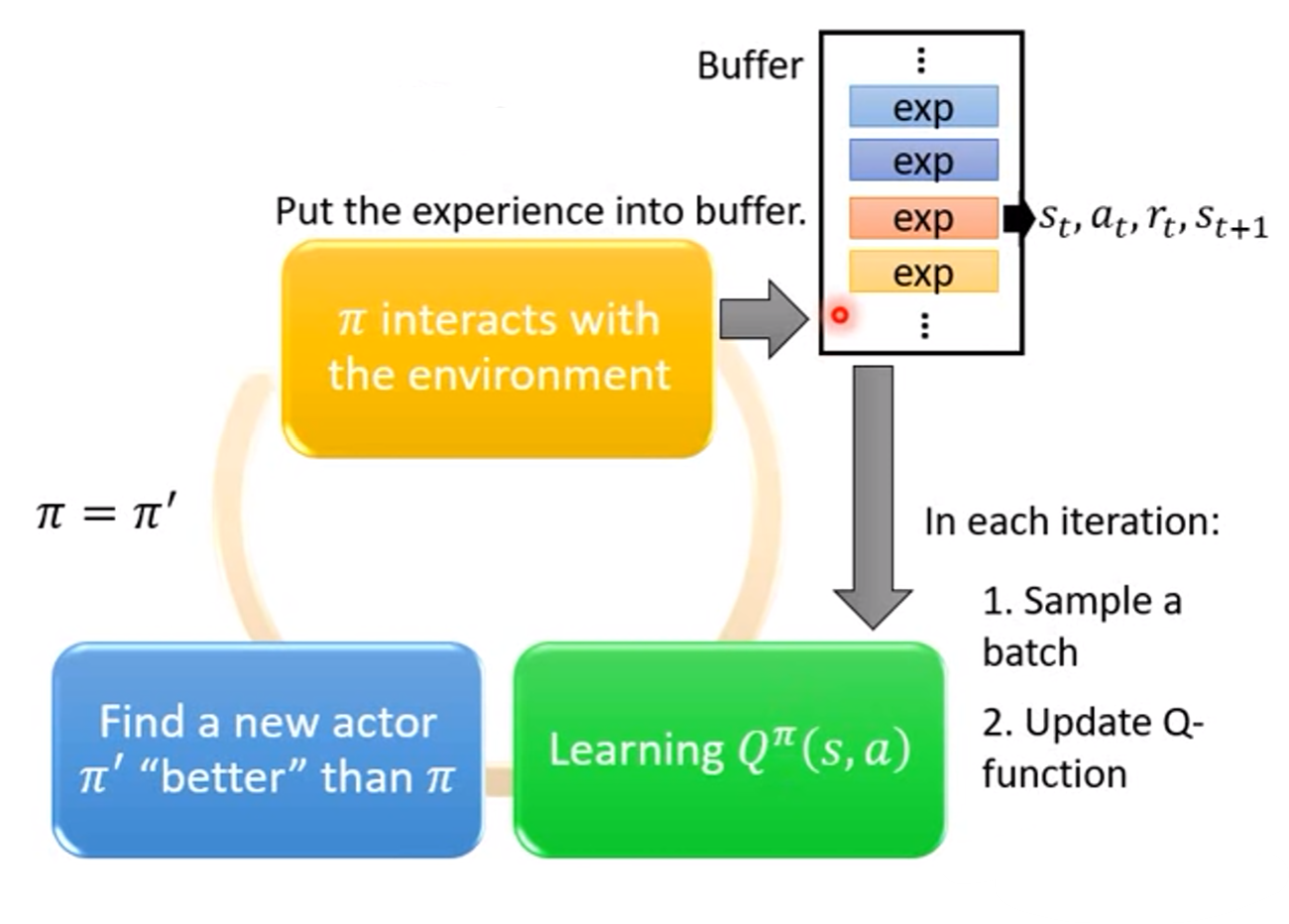
Q-learning整个算法的典型流程总结如下：

Q-Learning 还有很多高级的技巧，比如Double DQN等，但是这里就不展开讲了。

Version 3.5

除了Q-learning之外，critic还有什么用呢？我们在policy gradient version 3中说过累积奖励需要减去一个baseline $b$ 才能更好地判断一个行为究竟是好还是不好。但是，这个baseline $b$该怎么选取呢？其中一个好的办法就是减去$V^{\theta}(s_N)$。

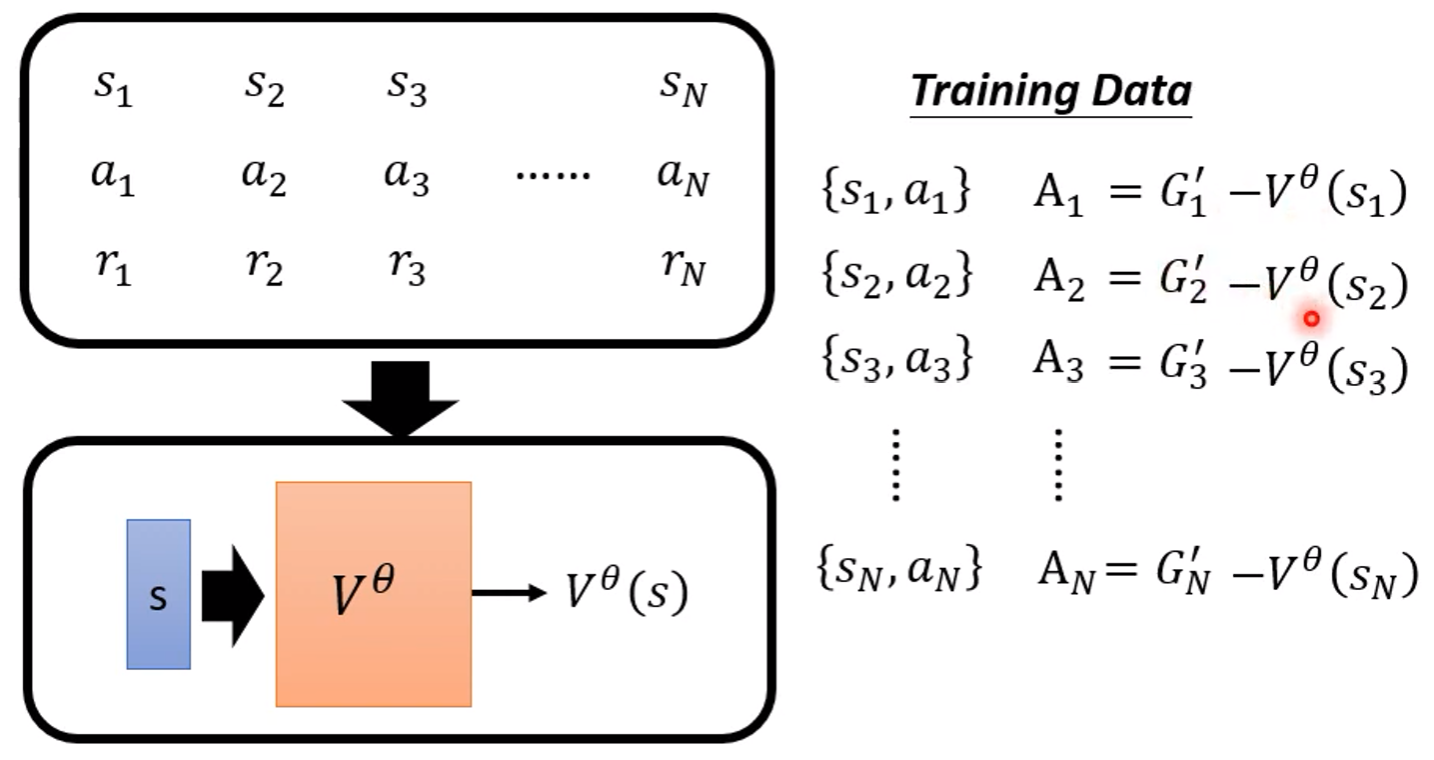
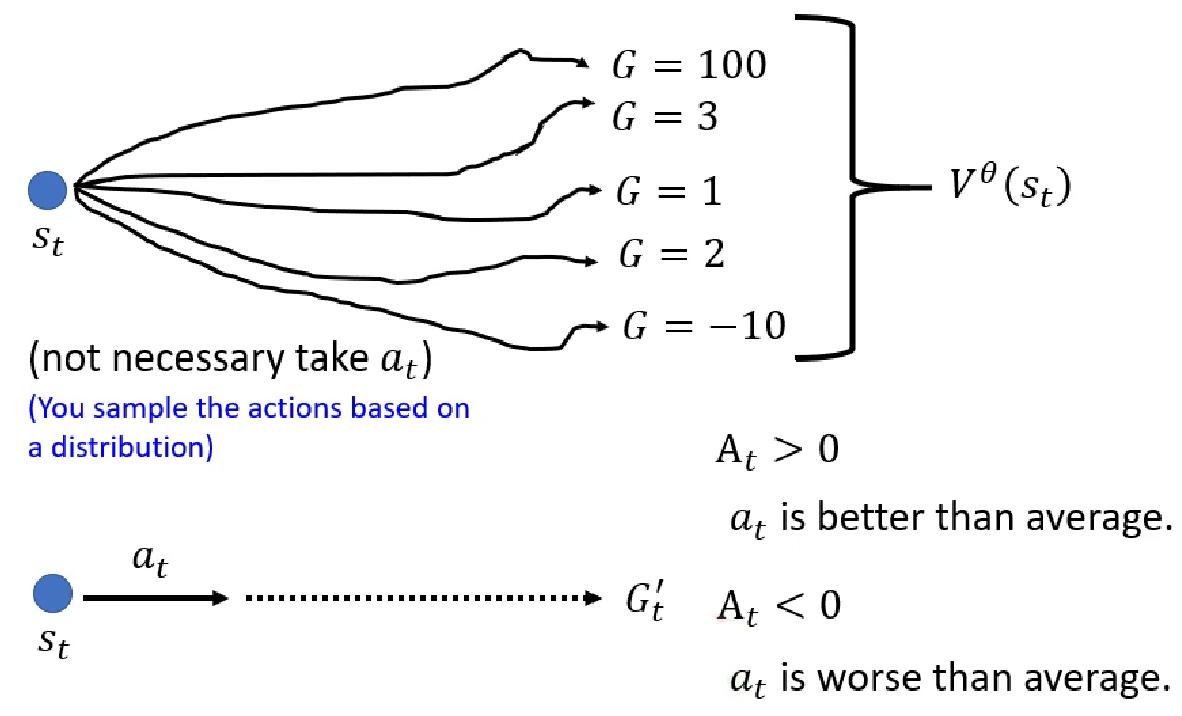
为什么说累积奖励$G^{'}_{t}$ 减去$V^{\theta}(s_t)$是更合理的选择呢？在观测到状态$s_t$之后，如果采取不同的动作，我们可以得到不同的累积奖励，其实$V^{\theta}(s_t)$是不同累积奖励的均值，是期望的累积奖励。所以，如果观测到状态$s_t$之后采取动作$a_t$得到的累积奖励$G^{'}_{t}$，我们计算$A_t=G^{'}_{t} - V^{\theta}(s_t)$，如果$A_t > 0$，说明这时候选择动作$a_t$要比平均值要好，反之，如果$A_t < 0$，说明选择动作$a_t$要比平均值要差。

Version 4

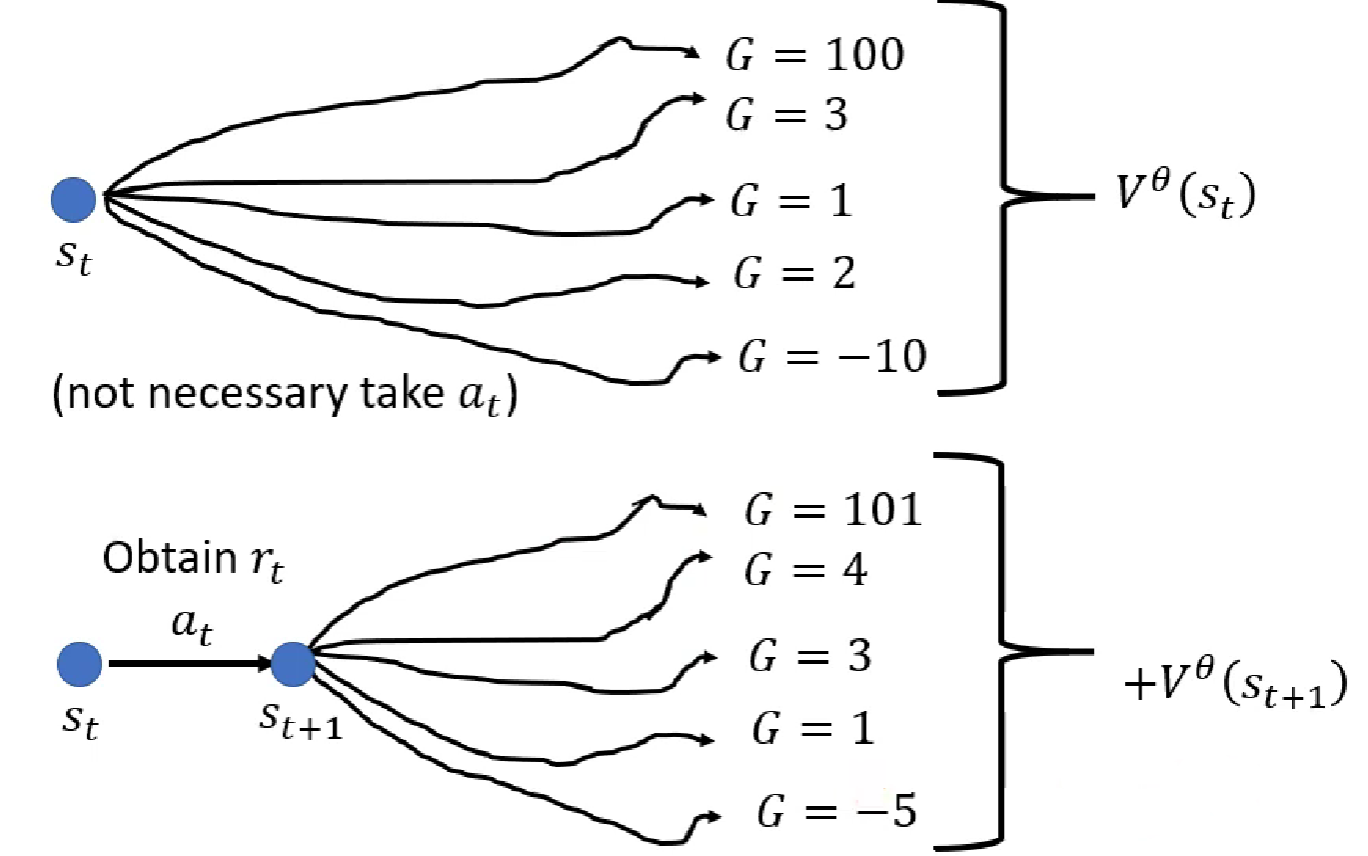
其实，version 3.5 还有一个问题。那就是$G^{'}_{t}$只是一次抽样得到的累积奖励，去要拿去减一个均值，所以不太合理，解决方案就是我们的version 4。我们观测到的数据是$\{...s_t,a_t,r_t,s_{t+1}\}$，当我们训练好一个critic之后，我们可以求得$V^{\theta}(s_{t+1})$，它是观测到状态$s_{t+1}$之后的期望累积奖励。所以说观测到状态$s_t$之后采取动作$a_t$得到的累积奖励应该是$r_t + V^{\theta}(s_{t+1})$。那么，$A_t$的计算方式变成了$A_t = r_t + V^{\theta}(s_{t+1}) - V^{\theta}(s_t)$。Version 4 就是著名的Advantage Actor-Critic。

强化学习中其他相关主题

Reward Shaping

Reward shaping就是针对奖励稀疏的强化学习问题，做法就是人为去设置一些奖励来加速学习。

Inverse Reinforcement Learning

更进一步，加入奖励已经不是稀疏的问题了，而是根本就没有reward，也不知道该怎么人为去设置reward，这种情况该怎么办呢？这就是inverse reinforcement learning要解决的问题。

没有reward，就不知道我们的actor跟环境的互动怎么样，那就没办法通过试错去学习了。那该怎么办呢？虽然没有reward，但是我们有人类的智慧，我们知道该怎么去解决一个问题，那么actor去学习我们怎么解决问题行不行呢？就比如说我们人类会开车，那么我们演示一遍，那actor能不能去模仿学会开车呢？答案是可以的。

但是等等，让actor模仿人类的行为，人类的行为不就是ground-truth吗？那这是一个监督学习吗？是的，这是监督学习，也就是所谓的Behavior Cloning。

但是Behavior Cloning存在两个问题，第一个就是人类不会演示失败的案例，比如翻车，那么actor也就不会处理失败的情况；第二个就是人类演示可能存在一些个人行为习惯的东西，这些东西跟任务完全无关，但是actor也会照搬过去，这是不合理的。Inverse reinforcement learning应运而生。

在这个问题中，我们有人类专家的经验、但是不知道怎么去定义奖励函数，还要避免actor完成照搬人类的行为，那么既然我们不知道奖励函数，能够能不能根据人类专家的经验去用机器学习学出一个奖励函数，然后用这个奖励函数去指导actor学习呢？这就是Inverse reinforcement learning。

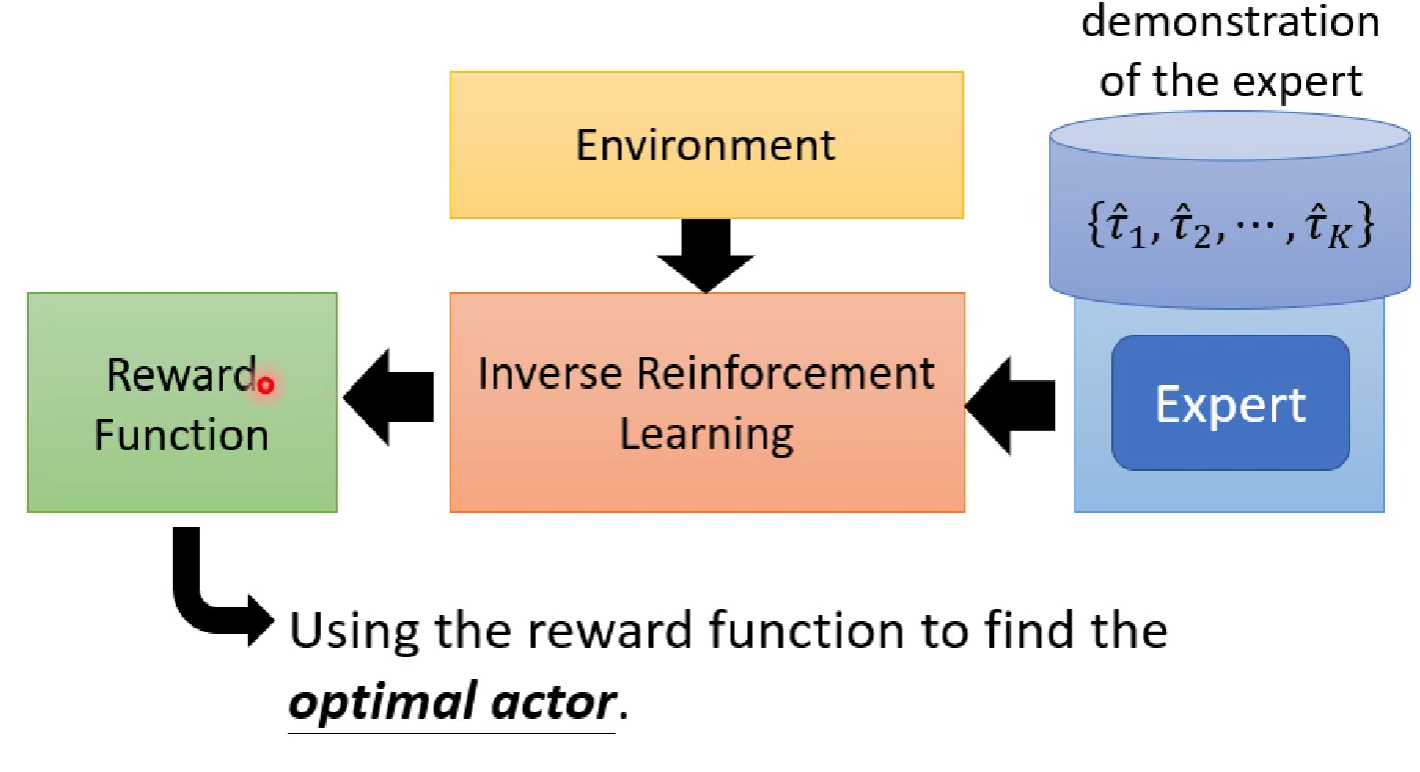
我们怎么去根据人类专家的经验反推除一个奖励函数呢？其中一个最基本的原则是：老师（人类专家）的行为总是最好的。根据这个原则设计的inverse reinforcement learning过程如下：

首先，初始化一个actor，然后让这个actor去跟环境互动，在每一个迭代中，先根据互动收集数据，然后定义一个奖励函数，要求这个奖励函数给老师的分数要高于actor的分数，然后这个actor基于这个奖励函数尝试最大化累积奖励，最终我们就得到了一个奖励函数以及训练好的actor。

整个inverse reinforcement learning的框架如下图所示，

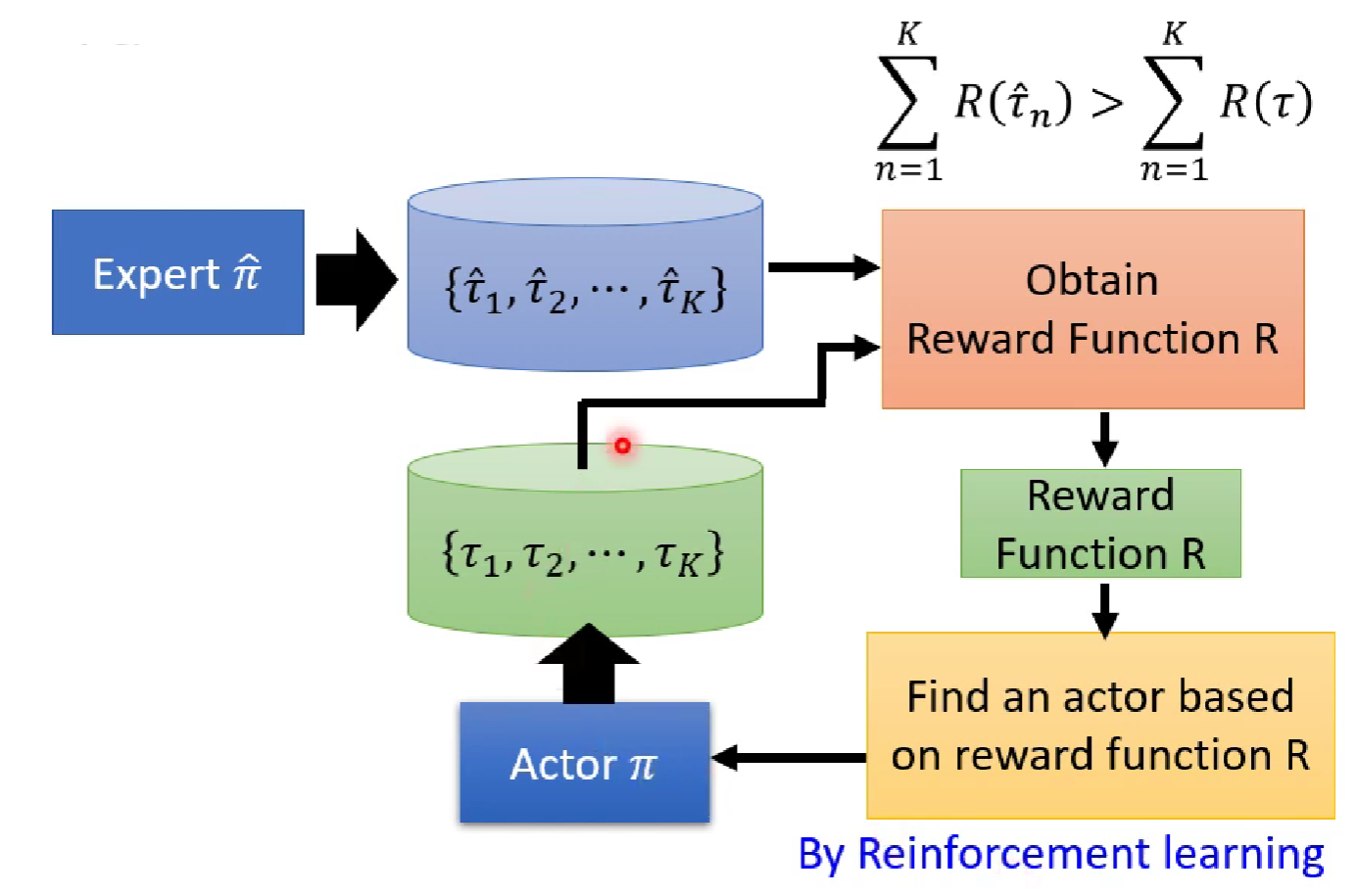
强化学习处理连续动作问题

需要注意的是前面我们讲的例子中都是默认actor可采取的动作空间都是离散的，如在玩space invader这个游戏的时候，可采取的动作只有左、右和开火，如下图所示。

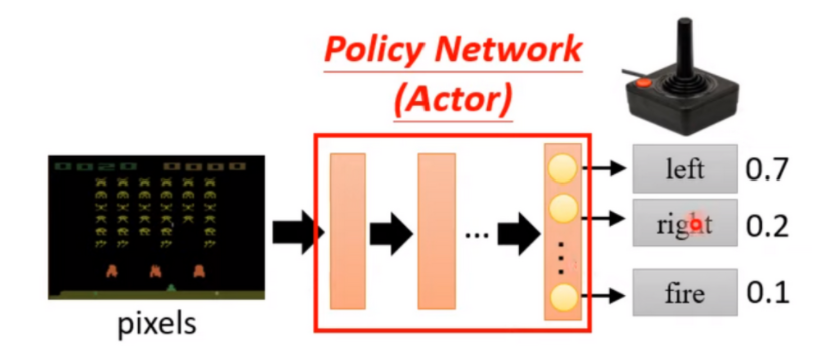
然后，我们可以通过$a=arg\ \underset{a}{max}\ Q(s,a)$ 最大化$Q\ Value$来选取最优的动作。但是，在实际应用中actor的动作空间却是连续的，例如在自动驾驶中方向盘转向的角度、油门的开度或者机器人关节的方向等。为什么动作空间连续对深度强化学习是一个问题呢？因为在神经网络架构设计中，往往是有多少个离散动作就有多少个输出神经元，但是如果动作空间是连续的，那我们该怎么设计输出神经元呢？今天，我们要考虑的就是怎么处理这样的问题。

Solution 1：

第一个直观方案就是连续问题离散化。这个方案是可行的，因为假设在自动驾驶里面方向盘应该向右打15度不会因为我打了16度而翻车。连续问题离散化方案通过在连续动作空间中抽样一组动作$\{ a_1,a_2,...,a_N \}$ ，例如下图是正态分布，通过抽样从而讲连续问题转换成了离散问题。

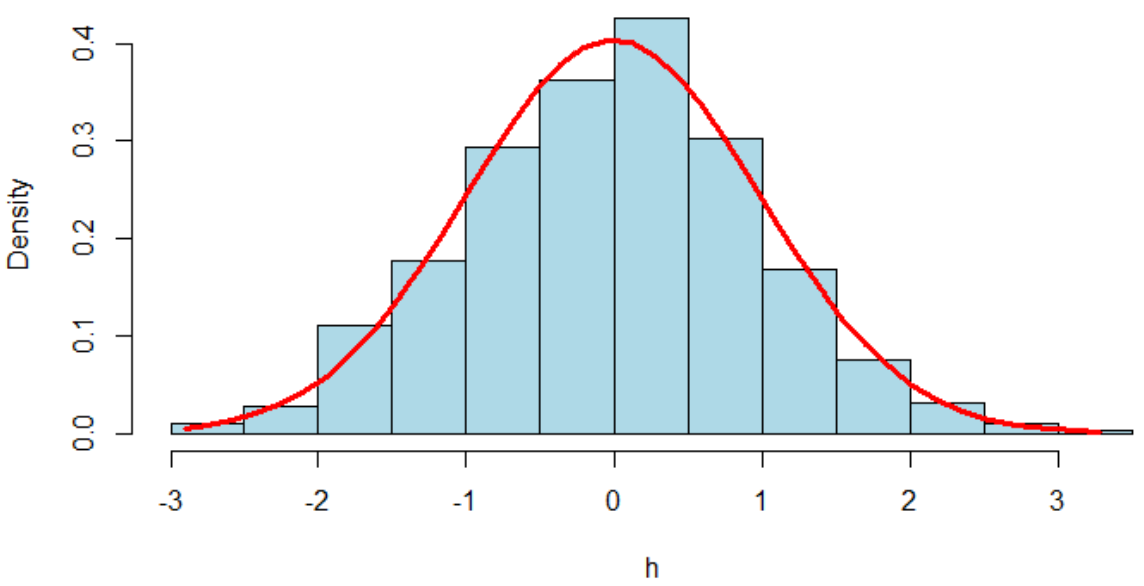
缺点：抽样的数量$N$需要足够大才会比较准确，但是数量太大会导致计算复杂度上升。

Solution 2：

第二个方案是把它当作回归（regression）问题来解。回归问题就是可以解决连续问题啊，只不过这样的话就需要每个动作设计一个网络，然后用梯度下降来解。

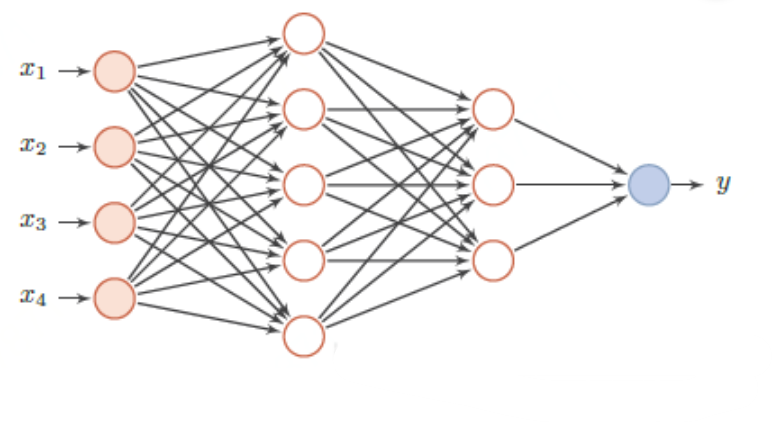
Solution 3：

对于连续动作空间 我们将每个动作的概率分布定义为一个高斯概率分布


假设我们有一个机器人，有K条机械腿，控制每条腿的弯曲角度来控制机器人前进或后退或拐弯。（在强化学习的目标就是跑到某一区域）

所以此时我们有K个动作。

对于这K个动作，存在k个均值和方差，来描述每个动作的概率分布（不同位置的机械腿 功能不同 自然不等价）。

那么如何得到这k组均值和方差呢？

依旧交给神经网络来完成。