chenjie04's blog

论文地址：Efficient Non-Local Contrastive Attention for Image Super-Resolution
代码地址：https://github.com/Zj-BinXia/ENLCA

Non-Local Contrastive Attention， 高效的非局部对比注意力 [1]！发表于AAAI 2022，属于空间注意力，用于单图像超分辨率任务。Non-Local Attention，译为非局部注意力，也就是全局注意力，通过利用自然图像中的内在特征相关性可以有效提升超分辨率的性能。但是Non-Local Attention由于自身的局限性，给图像中的噪声信息也分配了较大的权重，如下图所示，

其中，(a)是输入的原图，(b)是图(a)中红点与所有位置的Non-Local Attention权重，可以看到Non-Local Attention给不相干的特征也分配了很大的权重；图(c)是另外一种注意力机制 Non-Local Sparse Attention （$NLSA$） [2]分配的注意力权重，$NLSA$采用局部敏感哈希（Locality Sensitive Hashing (LSH)）将感受野限制在红点周围，可以看到$NLSA$计算的权重更加准确，但是由于受限的感受野，它忽略了很多重要的特征；图(d)是本文提出的Non-Local Contrastive Attention计算的权重，可以看到它不仅计算的权重更加精准同时也具有全局的感受野，简直牛逼！

Non-Local Attention

Non-Local Attention 可以通过从整个图像中聚合相关特征来学习表征，一般而言，定义如下：

$\textbf{Y}_{i} = \sum_{j=1}^{N} \frac{exp(\textbf{Q}_{i}^{\top} \textbf{K}_{j})}{\sum_{\hat{j}=1}^{N} exp(\textbf{Q}_{i}^{\top} \textbf{K}_{\hat{j}})} \textbf{V}_{j},$

$\textbf{Q} = \theta (\textbf{X}), \textbf{K} = \delta (\textbf{X}), \textbf{V} = \varphi (\textbf{X}),$

实际上这就是self-attention的一般实现形式，$\textbf{X} \in \mathbb{R}^{c \times N }$ 为输入的特征图，其中$N = h \times w$； $\theta (.)$，$\delta (.)$，$\varphi (.)$ 为对应的线性映射函数；$\textbf{Q}_{i}, \textbf{K}_{j} \in \mathbb{R}^{c}, \textbf{V}_{j} \in \mathbb{R}^{c_{out}}$ 则是对应特征图$\textbf{Q}, \textbf{K}, \textbf{V}$在位置$i, j$上的特征。

Non-Local Attention 第一个众所周知的缺点是其对输入尺寸二次方的复杂度，所以本文考虑的第一个点就是提升计算效率，作者考虑的是采用用核方法（Kernel Method） 去逼近Non-local Attention里面的指数函数。

Kernel Method

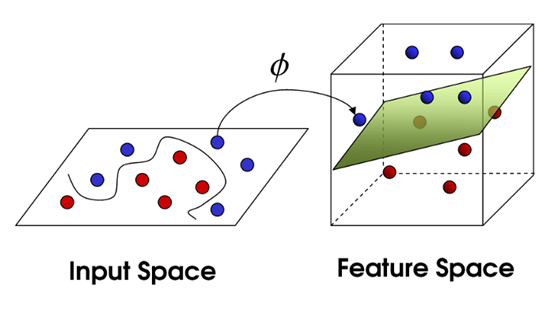
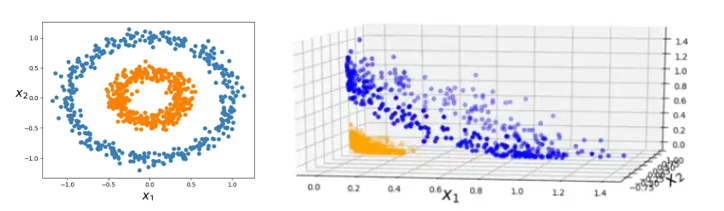
首先，机器学习分类任务中存在这么一个观察：低维空间中线性不可分的点映射到高维空间之后可能就线性可分了，所以按照这个思路，我们就应该把低维空间的点映射到高维空间再进行分类，因为在高维空间中是线性可分的。

对于线性模型$f(\textbf{x})=\textbf{w}^{\top}\textbf{x}$，其最优解是所有数据样本的线性组合$\textbf{w}^{*}=\sum^{N}_{i=i} \alpha _{i} \textbf{x}_{i}$，因此模型的最优解表示为：

$f^{*}(\textbf{x})=\sum_{i=1}^{N} \alpha _{i} \textbf{x}_{i}^{\top} \textbf{x}$

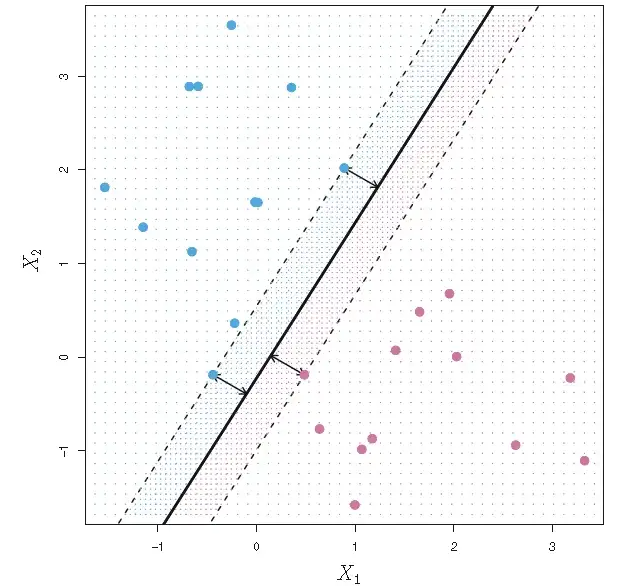
其实，对核方法理解的难点就在于这里：为什么线性模型的最优解是所有数据样本的线性组合？如果要严格去理论证明这件事可能需要用到表示定理（representer theorem）或者拉格朗日乘子法等知识，这些我已经忘得差不多了，以后再补补吧！在这里，我们举例子简单理解一下，例如在二维空间中，如下图所示有正负两类样本，其中分类边界就是中间的那条线，在线的这边属于一类，另一边属于另一类。显然，这条线是可以有所有数据样本线性组合得到的，分类的关键是怎么对这些数据样本进行线性组合，当然也不是所有的数据样本都对这条分类边界有用。在这里我们不讨论这些，只需要理解分类边界可以由所有数据样本线性组合得到，这样我们就将求权重$w^{*}$变成了求线性系数$\alpha$，可以采用梯度下降等方法求解。

但是，对于开头提到的低维空间中线性不可分的情况，我们就需要将其映射到高维空间中，即引入映射 $\phi : \mathcal{X} \to \mathcal{H}$将样本空间$\mathcal{H}$变换到高维的特征空间$\mathcal{F}$，所以模型最优解实际应该写成：

$f^{*}(\textbf{x})=\sum_{i=1}^{N} \alpha _{i} \phi(\textbf{x}_{i})^{\top} \phi(\textbf{x})$

但是，特征变换映射$\phi(\textbf{x})$是怎么样的啊？高维空间中$\phi(\textbf{x}_{i})^{\top} \phi(\textbf{x})$又该怎么求啊？对于这种需要将低维空间映射到高维空间并求高维空间中内积$\phi(\textbf{x})^{\top} \phi(\textbf{x}^{'})$ 的问题，我们就可以采用核方法（kernel method）。

我们先来看一个简单的例子：

还是一个二维映射到三维的例子，我们假设映射函数为：

$\phi(\textbf{x})=\phi(\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}) = \begin{pmatrix}x_{1}^{2}\\\sqrt{2} x_{1} x_{2} \\ x_{2}^{2}\end{pmatrix}$

那么，假如我们现在要求向量$\textbf{a},\textbf{b}$映射到三维空间后的内积，则

$\phi(\textbf{a})^{\top} \cdot \phi(\textbf{b}) = \begin{pmatrix}a_{1}^{2}\\\sqrt{2} a_{1} a_{2} \\ a_{2}^{2}\end{pmatrix} \cdot \begin{pmatrix}b_{1}^{2}\\\sqrt{2} b_{1} b_{2} \\ b_{2}^{2}\end{pmatrix}=a_{1}^{2}b_{1}^{2}+2a_{1}b_{1}a_{2}b_{2}+a_{2}^{2}b_{2}^{2} \\ =(a_{1}b_{1}+a_{2}b_{2})^{2} = (\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}^{\top} \cdot \begin{pmatrix}b_{1}\\b_{2}\end{pmatrix})^{2}=(\textbf{a}^{\top} \cdot \textbf{b})^{2}$

也就是说两个向量映射到三维空间后的内积实际上等于其在二维空间中的内积的平方，我们把$k(\textbf{a}，\textbf{b})=\phi(\textbf{a})^{\top} \cdot \phi(\textbf{b})$称为核函数，在这里其等于$(\textbf{a}^{\top} \cdot \textbf{b})^{2}$，也就是说加入我们知道了核函数，那我们压根就不需要先做特征映射再计算高维空间中的内积，而是直接再低维空间中直接就可以求出高维空间中的内积了。

核函数定义： 设$\mathcal{X}$是输入空间（欧式空间$\mathbf{R}^{n}的子集或离散集合$），又设$\mathcal{H}$为特征空间（希尔伯特空间），如果存在一个从$\mathcal{X}$到$\mathcal{H}$的映射：

$\phi : \mathcal{X} \to \mathcal{H}$

使得对所有$\textbf{x},\textbf{z} \in \mathcal{X}$，函数$k(\textbf{x},\textbf{z})$满足条件

$k(\textbf{x},\textbf{z}) = \phi(\textbf{x}) \cdot \phi(\textbf{z})$

则称$k(\textbf{x},\textbf{z})$为核函数，$\phi(\textbf{x})$为映射函数，式中$\phi(\textbf{x}) \cdot \phi(\textbf{z})$为$\phi(\textbf{x})$和$\phi(\textbf{z})$的内积。

最后一个问题：核函数怎么来的呢？随便写的吗？有人说核函数的确定并不困难，满足Mercer定理的函数都可以作为核函数，但是我不会。我只知道一些常用的核函数。

常见核函数如下：

（1）线性核函数：

$k(\textbf{x},\textbf{z})=\textbf{x}^{\top}\textbf{z}$

（2）多项式核函数：

$k(\textbf{x},\textbf{z})=(\zeta + \gamma \textbf{x}^{\top}\textbf{z})^{q}, \zeta \ge 0, \gamma >0$

（3）高斯核函数

$k(\textbf{x},\textbf{z})= exp(-\gamma||\textbf{x}-\textbf{z}||^{2})$

（4）拉普拉斯核函数

$k(\textbf{x},\textbf{z})= exp(-\frac{||\textbf{x}-\textbf{z}||}{\sigma})$

（5）……

对于一个核函数，总能找到一个对应的映射$\phi(\cdot)$，即任何核函数都隐式地定义了一个称为再生核希尔伯特空间(reproducing kernel Hilbert space)的特征空间，通常希望样本在特征空间内是线性可分的，选择核函数相当于选择了特征空间。

核方法是一种手段，一种trick，所以也叫kernel trick。Kernel trick 适合用于解决此类需要将低维输入空间映射到高维特征空间且目标函数包含映射后高维特征向量内积的问题，kernel trick可以直接用核函数直接替代内积，甚至不用知道映射函数$\phi(\textbf{x})$。

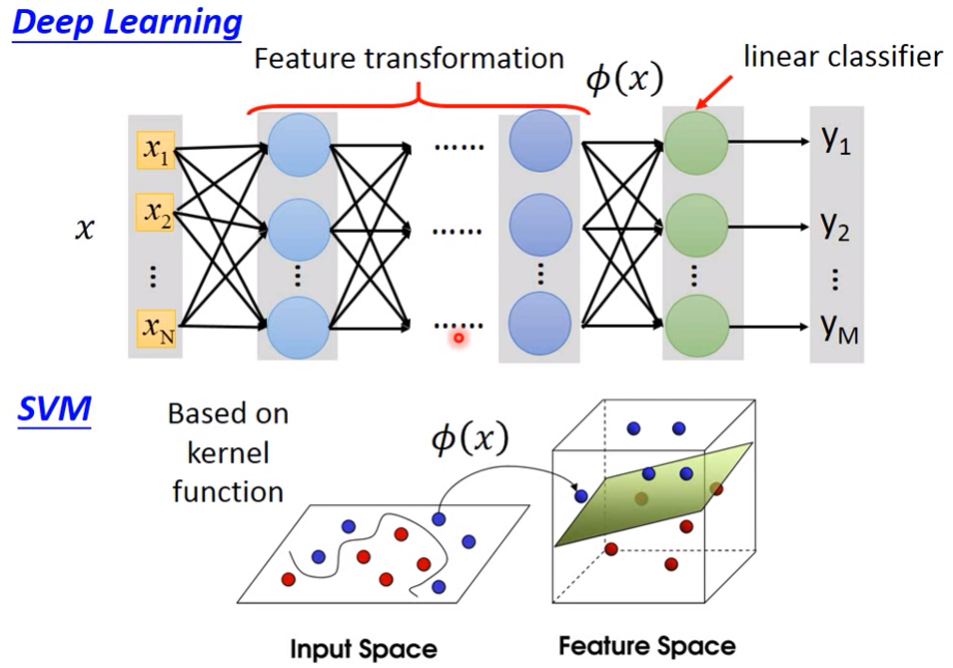
Kernel trick可以说是经典机器学习方法中一种非常漂亮的理论了，这里只能给出一个粗浅的理解，深入理解请参考网上的教程 [3]。用到kernel trick的比较经典的机器学习方法就是SVM了，详情请参考大佬的文章[4]。最后提一句深度学习与kernel-based方法的区别，如下图所示，深度学习实际上真的就是把低维空间的点映射到高维空间再进行分类，在Efficient Non-Local Contrastive Attention这篇文章中作者也是这样用的。

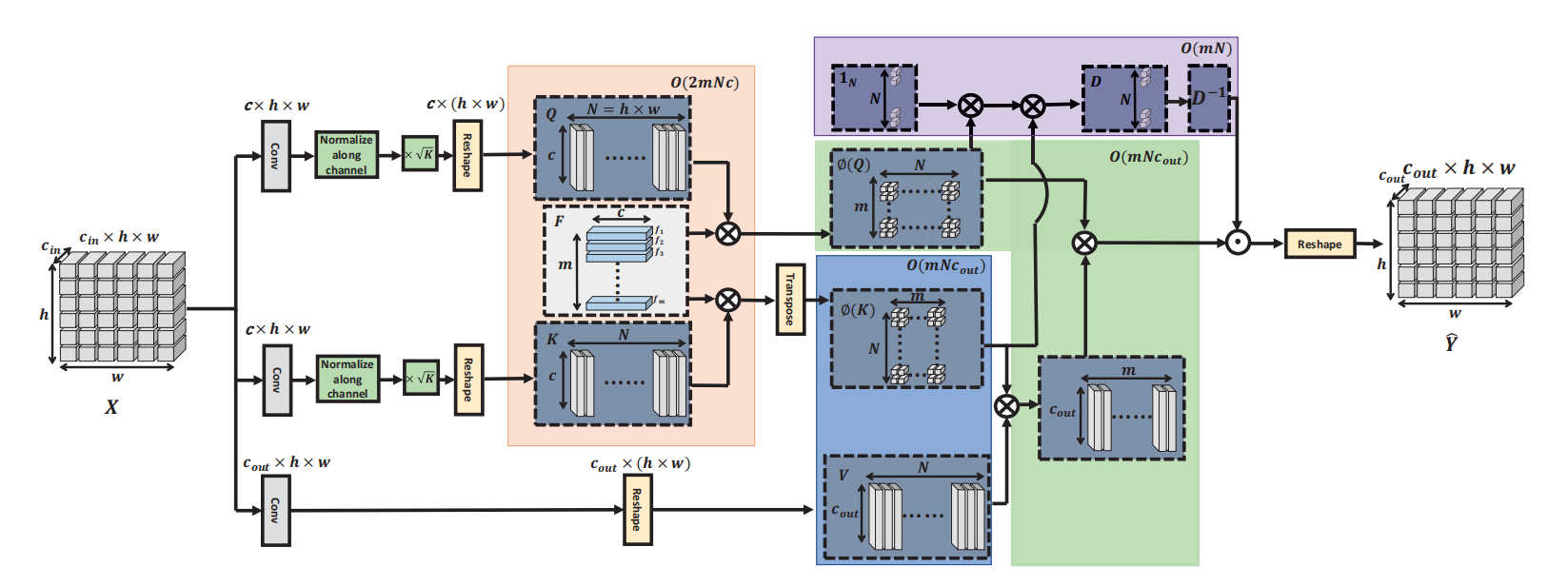
Efficient Non-Local Attention

Efficient Non-local Attention的架构如上图所示，为了给相干的特征更大的权重，忽略不相干特征，作者给输入的$\textbf{Q}$和$\textbf{K}$乘上一个放大因子$k$（说实在的，我并不理解为啥乘上$k$就能达到目的，可能是比如一个权重的$0.1$，一个是$0.9$，假如同时乘上6倍，变成了$0.6 : 5.4$，虽然比率不变，但是数量级不一样了，算是增强了权重的离散度，也就是归一化（Normalization）的反向运用），在实现上就是在做线性映射的时候给$\textbf{Q}$和$\textbf{K}$分别乘上一个$\sqrt{k}$，即：

$\textbf{Q} = \sqrt{k} \frac{\theta (\textbf{X})}{||\theta (\textbf{X})||}, \textbf{K} = \sqrt{k} \frac{\delta (\textbf{X})}{||\theta (\textbf{X})||}, \textbf{V} = \varphi(\textbf{X}),$

作者考虑用核方法（Kernel Method） 去逼近Non-local Attention里面的指数函数。那么设核函数为：

$\begin{aligned} &\ K(\textbf{Q}_{i}, \textbf{K}_{j}) = exp(\textbf{Q}_{i}^{\top} \textbf{K}_{j}) \\ &=exp((||\textbf{Q}_{i}+\textbf{K}_{j}||^{2} - |\textbf{Q}_{i}||^{2} - ||\textbf{K}_{j}||^{2}) / 2) \\ &=exp(- (||\textbf{Q}_{i}||^{2}+||\textbf{K}_{j}||^{2}) / 2) exp(||\textbf{Q}_{i}+\textbf{K}_{j}||^{2} / 2) \\ \end{aligned}$

定义高斯随机样本为$\textbf{f} \in \mathbb{R}^{c}$且$\textbf{f} \sim \mathcal{N}(\textbf{0}_{c},\textbf{I}_{c})$，则对任意$\textbf{Q}_{i},\textbf{K}_{j} \in \mathcal{R}^{c}$有

$(2\pi)^{-c/2} \int exp(-||\textbf{f}-(\textbf{Q}_{i}+\textbf{K}_{j})||^{2} /2)d\textbf{f}=1$

(这个公式我没看懂！)，根据该公式，核函数中的$exp(||\textbf{Q}_{i}+\textbf{K}_{j}||^{2} / 2)$可以近似为：

$\begin{aligned} &exp(||\textbf{Q}_{i}+\textbf{K}_{j}||^{2} / 2) = (2\pi)^{-c/2} exp(||\textbf{Q}_{i}+\textbf{K}_{j}||^{2} / 2) \cdot \int exp(-||\textbf{f}-(\textbf{Q}_{i}+\textbf{K}_{j})||^{2} /2)d\textbf{f} \\ &=(2\pi)^{-c/2} \int exp(-||\textbf{f}||^{2}/2+\textbf{f}^{\top}(\textbf{Q}_{i}+\textbf{K}_{j})-||\textbf{Q}_{i}+\textbf{K}_{j}||^{2}/2+||\textbf{Q}_{i}+\textbf{K}_{j}||^{2} / 2) d \textbf{f}\\ &=(2\pi)^{-c/2} \int exp(-||\textbf{f}||^{2}/2+\textbf{f}^{\top}(\textbf{Q}_{i}+\textbf{K}_{j}))d \textbf{f}\\ &=(2\pi)^{-c/2} \int exp(-||\textbf{f}||^{2}/2) \cdot exp(\textbf{f}^{\top}(\textbf{Q}_{i}+\textbf{K}_{j})) d \textbf{f} \\ &= \mathbb{E}_{f \sim \mathcal{N}(\textbf{0}_{c},\textbf{I}_{c})} [exp(\textbf{f}^{\top}(\textbf{Q}_{i}+\textbf{K}_{j}))] \end{aligned}$

那么，核函数最终为：

$\begin{aligned} &\ K(\textbf{Q}_{i}, \textbf{K}_{j}) = exp(\textbf{Q}_{i}^{\top} \textbf{K}_{j})\\ &=exp(- (||\textbf{Q}_{i}||^{2}+||\textbf{K}_{j}||^{2}) / 2) exp(||\textbf{Q}_{i}+\textbf{K}_{j}||^{2} / 2) \\ &= \mathbb{E}_{f \sim \mathcal{N}(\textbf{0}_{c},\textbf{I}_{c})} exp(\textbf{f}^{\top}(\textbf{Q}_{i}+\textbf{K}_{j}) - \frac{||\textbf{Q}_{i}||^{2}+||\textbf{K}_{j}||^{2}}{2}) \\ &=\phi(\textbf{Q}_{i})^{\top} \phi(\textbf{K}_{j}) \end{aligned}$

在实作上，作者用了$m$个高斯随机样本，$\textbf{f}_{1}, \cdots, \textbf{f}_{m} \overset{i.i.d}{\sim} \mathcal{N}(\textbf{0}_{c},\textbf{I}_{c})$ 并拼接成高斯随机矩阵$\textbf{F} \in \mathbb{R}^{m\times c}$。根据上述核函数可知，指数函数$exp(\textbf{Q}_{i}^{\top} \textbf{K}_{j})$可由映射后的向量内积$\phi(\textbf{Q}_{i}^{\top})\phi(\textbf{K}_{j})$近似，而映射函数为：

$\phi(\textbf{u}) = \frac{1}{\sqrt{m}} exp(-||\textbf{u}||^{2}/2) exp(\textbf{F} \textbf{u})$

基于上述分解和矩阵结合律，Efficient Non-Local Attention可以表示为：

$\hat{\textbf{Y}} = \textbf{D}^{-1}(\phi(\textbf{Q})^{\top}(\phi(\textbf{K})\textbf{V}^{\top})), \\ \textbf{D} = diag [\phi(\textbf{Q})^{\top}(\phi(\textbf{K})\textbf{1}_{N})]$

整个Efficient Non-Local Attention模块的实现师姐可以参考上图。经过上述改造，整个模块的复杂度为$\mathcal{O}(2mNc+2mNc_{out}+mN)$。

Efficient Non-Local Attention还存在一个问题，即随着核函数$K(\textbf{Q}_{i}, \textbf{K}_{j})$的增长，$\phi(\textbf{Q}_{i})^{\top} \phi(\textbf{K}_{j})$的方差成指数增长，

$\begin{aligned} Var(\phi(\textbf{Q}_{i})^{\top} \phi(\textbf{K}_{j})) &= \frac{1}{m} exp(-(||\textbf{Q}_{i}||^{2} + ||\textbf{K}_{j}||^{2})) Var(exp(\textbf{f}^{\top}(\textbf{Q}_{i}+\textbf{K}_{j}))) \\ &=\frac{1}{m} K^{2}(\textbf{Q}_{i}, \textbf{K}_{j}|)(exp(||\textbf{Q}_{i}+\textbf{K}_{j}||^{2})-1) \end{aligned}$

所以放大因子$k$不能太大，不然近似误差就会变大。但是为了进一步增加相干特征和不相干特征的差距( to further separate relevant and irrelevant features)，作者采用对比学习( contrastive learning)拉大相干特征与不相干特征的距离。

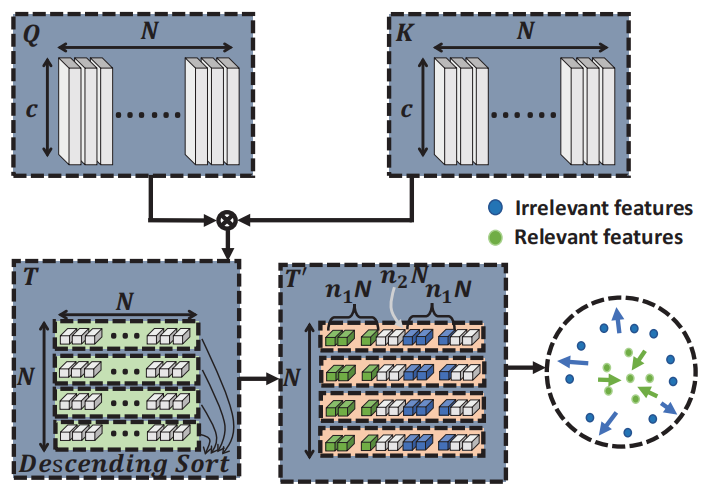
Contrastive Learning for Sparse Aggragation

整个对比学习方案如下图所示：

对于Query矩阵$Q$和Key矩阵$K$，首先度量两两之间的相似度，

$\textbf{T}_{i,j} = k \frac{ \textbf{Q}_{i}^{\top}}{ || \textbf{Q}_{i} || } \frac{\textbf{K}_{j}}{||\textbf{K}_{j}||}, k > 1, \textbf{T}_{i,j} \in \textbf{T},$

然后对相似度向量$\textbf{T}_{i}$的元素进行排序，即从最相干到最不相干排序

$\textbf{T}_{i}^{'} = sort(\textbf{T}_{i}, Descending), \textbf{T}_{i}^{'} \in \textbf{T}^{'}, \textbf{T}_{i} \in \textbf{T}$

最后，设计对比学习的损失函数$\mathcal{L}_{cl}$为：

$\mathcal{L}_{cl} = \frac{1}{N} \sum_{i=1}^{N} - log \frac{\sum_{j=1}^{n_{1}N}exp(\textbf{T}_{i,j}^{'})/n_{1}N}{\sum_{n_{2}N}^{(n_{1}+n_{2})N}exp(\textbf{T}_{i,j}^{'})/n_{1}N} + b,$

$n_{1}$为选取的相干特征或不相干特征占的百分比，$n_{2}$为不相干特征的起始索引。通过最小化该损失函数就可以拉开相干特征与不相干特征的权重差距。

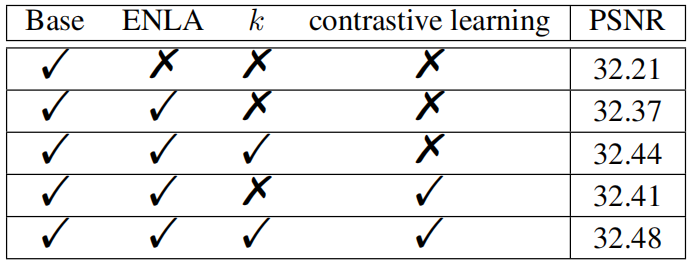
实验结果

Efficient Non-Local Contrastive Attention 的消融实验如下图所示，

将NLA替换为ENLA提升0.16，引入放大因子$k$则再增加0.7，使用对比学习增加0.4。

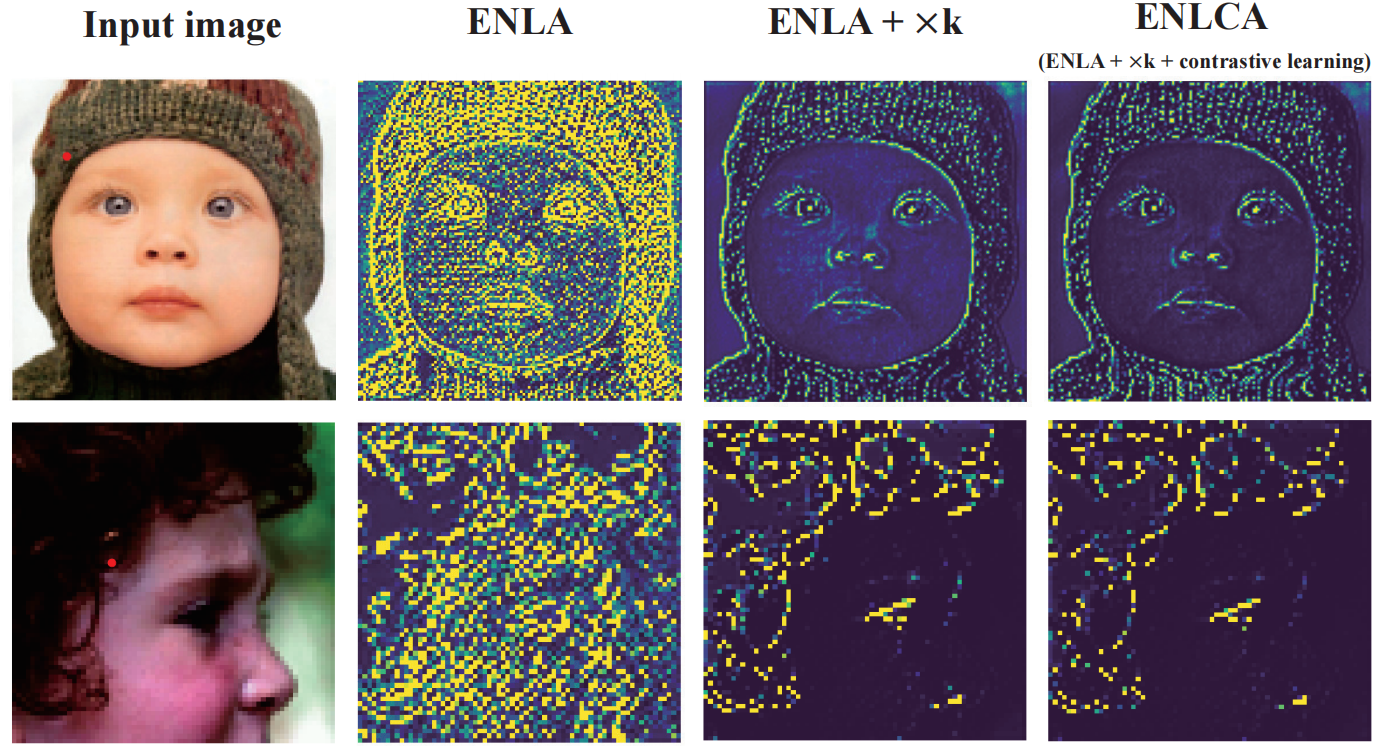
可视化效果如下图所示，

参考文献

[1] Xia B, Hang Y, Tian Y, et al. Efficient Non-Local Contrastive Attention for Image Super-Resolution[J]. arXiv preprint arXiv:2201.03794, 2022.
[2] Mei Y, Fan Y, Zhou Y. Image super-resolution with non-local sparse attention[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021: 3517-3526.
[3] https://0809zheng.github.io/2021/07/23/kernel.html
[4] https://blog.csdn.net/v_july_v/article/details/7624837